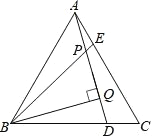
【题目】如图,在等边△ABC 中,点 D、E 分别在边 BC、AC 上,且 AE=CD,BE 与 AD 相交于点 P,BQ⊥AD 于点 Q.
(1)求证:BE=AD;
(2)若 PQ=4,求 BP 的长.
参考答案:
【答案】(1)见解析;(2)8.
【解析】
(1)欲证明BE=AD,只要证明△ABE≌△CAD即可;
(2)只要证明∠BPQ=60°,利用直角三角形30度角的性质即可解决问题.
证明:(1)∵△ABC为等边三角形,
∴AB=AC,∠BAC=∠C=60°,
在△ABE 和△CAD 中
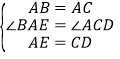 ,
,
∴△ABE≌△CAD(SAS),
∴BE=AD.
(2)∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BPQ=∠ABP+∠BAP=∠CAD+∠BAP=∠BAC=60°,
又∵BQ⊥AD,
∴∠BQP=90°,
∴∠PBQ=180°﹣∠BPQ﹣∠BQP=30°,
∴BP=2PQ,
又∵PQ=4,
∴BP=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=3,D、E分别是AB、AC上的点,且DE∥BC,将△ADE沿DE翻折,与梯形BCED重叠的部分记作图形L.
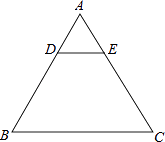
(1)求△ABC的面积;
(2)设AD=x,图形L的面积为y,求y关于x的函数解析式;
(3)已知图形L的顶点均在⊙O上,当图形L的面积最大时,求⊙O的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a>0)的图象与x轴交于A(x1 , 0)、B(x2 , 0)(x1<x2)两点,与y轴交于点C,x1 , x2是方程x2+4x﹣5=0的两根.
(1)若抛物线的顶点为D,求S△ABC:S△ACD的值;
(2)若∠ADC=90°,求二次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,把△ABC 纸片沿 DE 折叠,使点 A 落在四边形 BCED 的内部点 A′的位置,试说明 2∠A=∠1+∠2;
(2)如图②,若把△ABC 纸片沿 DE 折叠,使点 A 落在四边形 BCED 的外部点A′的位置,写出∠A 与∠1、∠2 之间的等量关系(无需说明理由);
(3)如图③,若把四边形 ABCD 沿 EF 折叠,使点 A、D 落在四边形BCFE 的内部点 A′、D′的位置,请你探索此时∠A、∠D、∠1 与∠2 之间的数量关系,写出你发现的结论并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:sin60°+|﹣5|﹣
 (4015﹣π)0+(﹣1)2013+(
(4015﹣π)0+(﹣1)2013+(  )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点.求证:BD=AE.

相关试题

