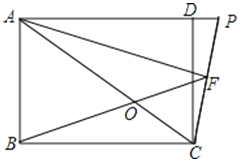
【题目】已知矩形ABCD中,AF为∠DAC的角平分线,CP⊥AF于点F,且交AD的延长线于P.连接BF交对角线AC于点O.

(1)若BC=4，tan∠ACB= ,求的值;

(2)求证:∠AOB=3∠PAF.

参考答案：

【答案】（1）-4，（2）证明见解析

【解析】

试题分析：（1）首先根据条件证明AP=AC，然后利用tan∠ACB=，求出AB=2，然后利用勾股定理求出AC=，DP=-4，再利用三角形的面积公式计算即可；（2）连接DF，根据（1）的过程得出PF=CF，进而得到∠ADF=∠BCF，然后证明△ADF≌△BCF，得出∠DAF=∠CBF，再利用角的和差关系可得出结论.

试题解析：（1）∵AF为∠DAC的角平分线，CP⊥AF，∴AP=AC，∵BC=4，tan∠ACB=，∴AB=2，根据勾股定理得AC=，∴DP=-4，∴S△DCP=DPDC=×（-4）×2=-4，

（2）如图所示，连接DF，

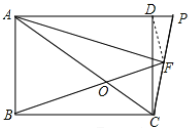
由（1）易知PF=CF，∴DF=CF，∴∠FDC=∠FCD，∴∠ADF=∠BCF，在△ADF和△BCF中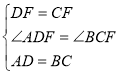，，∴△ADF≌△BCF，∴∠DAF=∠CBF，又∵∠ACB=∠DAC=2∠DAF，∴∠AOB=∠CBF+∠ACB=3∠DAF．

关闭