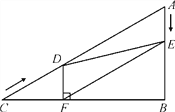
【题目】如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF。
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
参考答案:
【答案】(1)证明见解析;(2) 能,理由见解析;(3)见解析.
【解析】分析:(1)利用t表示出CD以及AE的长,然后在直角△CDF中,利用直角三角形的性质求得DF的长,即可证明;
(2)易证四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,据此即可列方程求得t的值;
(3)分两种情况讨论即可求解.
详解:(1)∵直角△ABC中,∠C=90°﹣∠A=30°.
∵CD=4t,AE=2t.
又∵在直角△CDF中,∠C=30°,∴DF=![]() CD=2t,∴DF=AE;
CD=2t,∴DF=AE;
(2)∵DF∥AB,DF=AE,∴四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,即60﹣4t=2t,解得:t=10,即当t=10时,AEFD是菱形;
(3)分两种情况讨论:
①当∠EDF=90°时,DE∥BC,∴∠ADE=∠C=30°,∴AD=2AE.
∵CD=4t,∴DF=2t=AE,∴AD=4t,∴4t+4t=60,∴t=![]() 时,∠EDF=90°.
时,∠EDF=90°.
②当∠DEF=90°时,DE⊥EF.
∵四边形AEFD是平行四边形,∴AD∥EF,∴DE⊥AD,∴△ADE是直角三角形,∠ADE=90°.
∵∠A=60°,∴∠DEA=30°,∴AD=![]() AE,AD=AC﹣CD=60﹣4t,AE=DF=
AE,AD=AC﹣CD=60﹣4t,AE=DF=![]() CD=2t,∴60﹣4t=t,解得t=12.
CD=2t,∴60﹣4t=t,解得t=12.
综上所述:当t=![]() 或t=12时,△DEF是直角三角形.
或t=12时,△DEF是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是一个菱形绿地,其周长为40
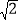 m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2,请问需投资金多少元?(结果保留整数)
m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2,请问需投资金多少元?(结果保留整数)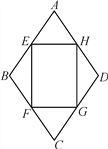
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)当运动3秒时,点M、N、P分别表示的数是 、 、 ;
(2)求运动多少秒时,点P到点M、N的距离相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格
﹣0.2
﹣0.1
0
0.1
0.2
0.5
筐数
5
8
2
6
8
1
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过顶点B,D作DE⊥a于点E,BF⊥a于点F,若DE=4,BF=3,则EF的长为( )
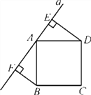
A. 1 B. 5 C. 7 D. 12
相关试题

