【题目】如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离 . 
参考答案:
【答案】(60+20 ![]() )米
)米
【解析】解:由题意可知:
∠ACP=∠BCP=90°,∠APC=30°,∠BPC=45°.
在Rt△BPC中,
∵∠BCP=90°,∠B=∠BPC=45°,
∴BC=PC=60.
在Rt△ACP中,
∵∠ACP=90°,∠APC=30°,
tan30°= ![]() ,
,
∴AC=PCtan30°=tan30°×60=60× ![]() =20
=20 ![]() (米).
(米).
∴AB=AC+BC=60+20 ![]() (米).
(米).
答:教学楼A与办公楼B之间的距离是(60+20 ![]() )米.
)米.
故答案是:(60+20 ![]() )米.
)米.
解直角三角形的基本方法就是把特殊角放在直角三角形中,利用边角关系BC=PC=60,AC=PCtan30°,求出AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,路灯距地面8米,身高1.6米的小明从距离灯底(点O)20米的点A处,沿AO所在直线行走12米到达点B时,小明身影长度( )

A.变长2.5米
B.变短2米
C.变短2.5米
D.变短3米 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算|﹣2|+(
 )﹣1×(π﹣
)﹣1×(π﹣  )2﹣
)2﹣  = .
= . -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立;请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是直线l上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:DF=EF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一蓄水池有水40m3,按一定的速度放水,水池里的水量y (m3)与放水时间t(分)有如下关系:
放水时间(分)
1
2
3
4
...
水池中水量(m)
38
36
34
32
...
下列结论中正确的是
A. y随t的增加而增大B. 放水时间为15分钟时,水池中水量为8m3
C. 每分钟的放水量是2m3D. y与t之间的关系式为y=38-2t
-
科目: 来源: 题型:
查看答案和解析>>【题目】父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:
距离地面高度(千米)h
0
1
2
3
4
5
温度(℃)t
20
14
8
2
﹣4
﹣10
根据表中,父亲还给小明出了下面几个问题,请你帮助小明回答下列问题:
(1)表中自变量是 ;因变量是 ;当地面上(即h=0时)时,温度是 ℃.
(2)如果用h表示距离地面的高度,用t表示温度,请写出满足t与h关系的式子.
(3)计算出距离地面6千米的高空温度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)尺规作图,不写作法,但要保留作图痕迹.
王师傅开车在一条公路上经过点B和点C处两次拐弯后继续前行,且前行方向CD和原来的方向AB相同,已知第一次的拐角为∠ABC,请借助圆规和直尺作出CD∥AB.
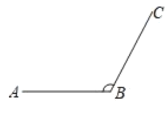
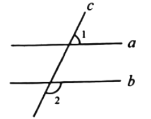
(2)如图,已知∠1+∠2=180°,请说明a∥b.
相关试题

