【题目】如图,在△ABC中,∠B=45°, ![]() ,等腰直角△DAE中,∠DAE=90°,且点D是边BC上一点。
,等腰直角△DAE中,∠DAE=90°,且点D是边BC上一点。
(1)求AC的长;
(2)如图1,当点E恰在AC上时,求点E到BC的距离;
(3)如图2, 当点D从点B向点C运动时,求点E到BC的距离的最大值。

图1 图2
参考答案:
【答案】(1)4(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)作AF⊥BC,垂足为F,由已知可得BF=AF=2,从而得CF=BC-BF=2![]() ,在Rt△FAC中,利用勾股定理即可求出AC长;
,在Rt△FAC中,利用勾股定理即可求出AC长;
(2)过点A作AB的垂线交BC于点G,连接EG,证明△BAD≌△GAE,从而得∠AGE=∠ABD=45°,EG=BD,继而得∠EGB=90°,得到点E到BC的距离为EG的长,设BD=x,则DF=2-x,CD=2![]() +2-x,在Rt△ADF中,AD2=AF2+DF2=22+(2-x)2, 在Rt△ADC中,AD2=CD2-AC2=(2
+2-x,在Rt△ADF中,AD2=AF2+DF2=22+(2-x)2, 在Rt△ADC中,AD2=CD2-AC2=(2![]() +2-x)2-42,从而解得x=
+2-x)2-42,从而解得x=![]() ,即得到点E到BC的距离;
,即得到点E到BC的距离;
(3)当点D从点B向点C运动时,由(2)知点E到BC的距离为EG的长,即为BD的长,从而得到最大值即为BC的长.
试题解析:(1)作AF⊥BC,垂足为F,
∵∠B=45°,∴△FBA为等腰直角三角形,
∴BF=AF,
∵AB=2![]() ,∴AF=BF=2,
,∴AF=BF=2,
∵BC=2![]() +2,∴CF=BC-BF=2
+2,∴CF=BC-BF=2![]() ,
,
在Rt△FAC中,AC=![]() =4;
=4;
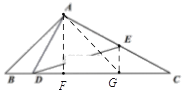
(2)过点A作AB的垂线交BC于点G,连接EG,
∵∠B=45°,∠BAG=90°,∴△GBA为等腰直角三角形,∴AB=AG, ∠AGB=45°,
∵∠DAE=90°,△DAE为等腰直角三角形,
∴AD=AE,∠BAD=∠GAE,∴△BAD≌△GAE,∴∠AGE=∠ABD=45°,EG=BD,
∴∠EGB=∠AGE+∠AGB=45°+45°=90°,故点E到BC的距离为EG的长,
设BD=x,则DF=2-x,CD=2![]() +2-x,
+2-x,
在Rt△ADF中,AD2=AF2+DF2=22+(2-x)2,
在Rt△ADC中,AD2=CD2-AC2=(2![]() +2-x)2-42,
+2-x)2-42,
∴22+(2-x)2=(2![]() +2-x)2-42,解得x=
+2-x)2-42,解得x=![]() ,
,
∴点E到BC的距离EG=BD=![]() ;
;
(3)当点D从点B向点C运动时,
由(2)可知△BAD≌△GAE,
∴∠AGE=∠ABD=45°,EG=BD,
∴∠EGB=∠AGE+∠AGB=45°+45°=90°,故点E到BC的距离为EG的长,
∵EG=BD,
∴当BD=BC=![]() 时,点E到BC的距离最大,最大值为
时,点E到BC的距离最大,最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形从一个顶点出发共有7条对角线,则这个多边形的边数为( )
A.8B.9C.10D.11
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划用104 000元购置一批电脑(这批款项须恰好用完,不得剩余或追加).经过招标,其中平板电脑每台1600元,台式电脑每台4000元,笔记本电脑每台4600元.
(1)若学校同时购进其中两种不同类型的电脑共50台,请你帮学校设计该如何购买;
(2)若学校同时购进三种不同类型的电脑共26台(三种类型的电脑都有),并且要求笔记本电脑的购买量不少于15台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点A,B,C所对应的数分别为m,n,2+n,当其中一点到另外两点的距离相等时,则m-n的值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l1的解析式为y=-x,直线l2与l1交于A点(a,-a)与,与y轴交于点B(0,b),其中a,b满足(a+2)2+
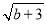 =0 .
=0 .(1)求直线l2放入解析式;
(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;
(3)已知平行于y轴且位于y轴左侧有一动直线,分别与
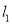 ,
, 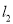 交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.
交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标. 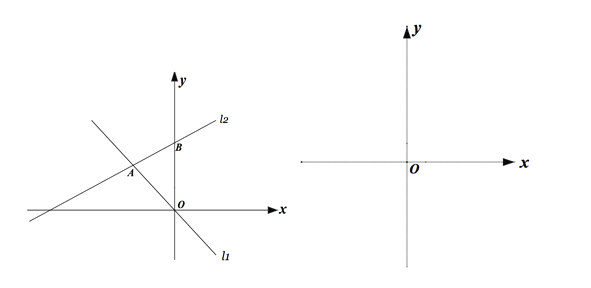
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了考查一批日光灯管的使用寿命,从中抽取了100只日光灯管进行试验,在这个问题中,①总体是指这批日光灯管的全体;②个体是指每只日光灯管的使用寿命;③样本是指从中抽取的100只日光灯管的使用寿命;④样本容量是100只灯管,说法正确的有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解广大市民对垃圾分类知识的了解程度,应采用的合适的调查方式为_________.(填普查或抽样调查)
相关试题

