【题目】如图,已知∠CAB=∠DAB,则添加下列一个条件不能使△ABC≌△ABD的是( ) 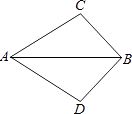
A.AC=AD
B.BC=BD
C.∠C=∠D
D.∠ABC=∠ABD
参考答案:
【答案】B
【解析】解:A、∵在△ABC和△ABD中 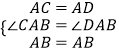
∴△ABC≌△ABD(SAS),正确,故本选项错误;
B、根据BC=BD,AB=AB和∠CAB=∠DAB不能推出两三角形全等,错误,故本选项正确;
C、∵在△ABC和△ABD中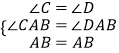
∴△ABC≌△ABD(AAS),正确,故本选项错误;
D、∵在△ABC和△ABD中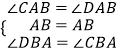
∴△ABC≌△ABD(ASA),正确,故本选项错误;
故选B.
全等三角形的判定定理有SAS,ASA,AAS,SSS,已知有∠DAB=∠CAB和隐含条件AB=AB,看看再添加的条件和以上两个条件是否符合全等三角形的判定定理即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
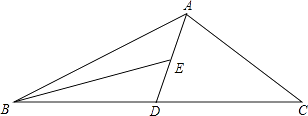
(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,M为BC边上的中点,D是射线AM上的一个动点,以CD为一边且在CD的下方作等边△CDE,连接BE.

(1)填空:若D与M重合时(如图1)∠CBE=度;
(2)如图2,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(1)的条件下,若AB=6,试求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2向左平移2个单位,所得抛物线的解析式为( )
A.y=x2﹣2B.y=x2+2C.y=(x+2)2D.y=(x﹣2)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2+∠3+∠4+∠5+∠6=度.
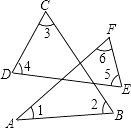
-
科目: 来源: 题型:
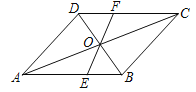
查看答案和解析>>【题目】如图所示,在□ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.
(1)求证:OE=OF;
(2)若AB=6,BC=5,OE=2,求四边形BCFE的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a+2a=3a2
B.aa2=a3
C.(2a)2=2a2
D.(﹣a2)3=a6
相关试题

