【题目】已知直线AB∥CD.
(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是 .
(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.
(3)如图3,点E在直线BD的右侧,BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系 .

参考答案:
【答案】(1)∠ABE+∠CDE=∠BED;(2)详见解析;(3)2∠BFD+∠BED=360°.
【解析】试题分析:(1)点E作EF∥AB,根据平行线的性质易证得∠1=∠ABE,∠2=∠CDE,则可得∠ABE+∠CDE=∠BED;(2)∠BFD=![]() ∠BED,已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=
∠BED,已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,所以∠ABF+∠CDF=
∠CDE,所以∠ABF+∠CDF=![]() ∠ABE+
∠ABE+![]() ∠CDE=
∠CDE=![]() (∠ABE+∠CDE),由(1)的结论可得∠BFD=∠ABF+∠CDF=
(∠ABE+∠CDE),由(1)的结论可得∠BFD=∠ABF+∠CDF=![]() (∠ABE+∠CDE),∠BED=∠ABE+∠CDE,所以∠BFD=
(∠ABE+∠CDE),∠BED=∠ABE+∠CDE,所以∠BFD=![]() ∠BED;(3过点E作EG∥CD,根据平行公理可得AB∥CD∥EG,根据平行线的性质易证∠ABE+∠CDE+∠BED=360°,再由(1)的方法可得∠BFD=∠ABF+∠CDF;已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=
∠BED;(3过点E作EG∥CD,根据平行公理可得AB∥CD∥EG,根据平行线的性质易证∠ABE+∠CDE+∠BED=360°,再由(1)的方法可得∠BFD=∠ABF+∠CDF;已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,所以∠BFD=
∠CDE,所以∠BFD=![]() (∠ABE+∠CDE),即2∠BFD+∠BED=360°.
(∠ABE+∠CDE),即2∠BFD+∠BED=360°.
试题解析:
(1)∠ABE+∠CDE=∠BED.
理由:如图1,作EF∥AB,
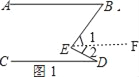
∵直线AB∥CD,
∴EF∥CD,
∴∠ABE=∠1,∠CDE=∠2,
∴∠ABE+∠CDE=∠1+∠2=∠BED,
即∠ABE+∠CDE=∠BED.
故答案为:∠ABE+∠CDE=∠BED.
(2)∠BFD=![]() ∠BED.
∠BED.
理由:如图2,∵BF,DF分别平分∠ABE,∠CDE,
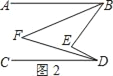
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() ∠ABE+
∠ABE+![]() ∠CDE=
∠CDE=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
由(1),可得∠BFD=∠ABF+∠CDF=![]() (∠ABE+∠CDE)
(∠ABE+∠CDE)
∠BED=∠ABE+∠CDE,
∴∠BFD=![]() ∠BED.
∠BED.
(3)2∠BFD+∠BED=360°.
理由:如图3,过点E作EG∥CD,
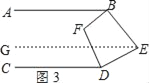
∵AB∥CD,EG∥CD,
∴AB∥CD∥EG,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠CDE+∠BED=360°,
由(1)知,∠BFD=∠ABF+∠CDF,
又∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠BFD=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
∴2∠BFD+∠BED=360°.
故答案为:2∠BFD+∠BED=360°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图数在线的A、B、C三点所表示的数分别为a、b、c.根据图中各点位置,判断下列各式何者正确( )

A. (a﹣1)(b﹣1)>0 B. (b﹣1)(c﹣1)>0 C. (a+1)(b+1)<0 D. (b+1)(c+1)<0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个数的绝对值等于本身,那么这个数是( )
A.正数B.0C.非正数D.非负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
若∠En=1度,那∠BEC等于 度

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.

(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题:大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用 来表示
来表示 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为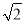 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2< <3,∴
<3,∴ 的整数部分为2,小数部分为
的整数部分为2,小数部分为 ﹣2.
﹣2.请解答:
(1)
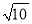 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .(2)如果
 的小数部分为a,
的小数部分为a,  的整数部分为b,求a+b-
的整数部分为b,求a+b- 的值;
的值;(3)已知:x是3+
 的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a﹣a=2B.5x﹣3x=2x
C.y2﹣y=yD.3a2+2a2=5a4
相关试题

