【题目】在ΔABC中,∠ABC的平分线与在∠ACE的平分线相交于点D.
(1)若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数.
(2)由(1)小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明.

参考答案:
【答案】答案见解析
【解析】试题分析:(1)根据三角形内角和定理和角平分线的性质,已知∠ABC=60°,∠ACB=40°,易求∠A和∠D度数.(2)根据三角形外角的性质以及角平分线性质,可得∠ACE=2∠D+∠ABC,∠ACE=∠A+∠ABC,即可得∠A和∠D的数量关系.
试题解析:解:(1)∵∠ABC=60°,∠ACB=40°,∴∠A=80°.
∵BD平分∠ABC,∠ABC=60°,
∴∠DBC=30°.
又∵∠ACB=40°,
∴∠ACE=140°.
又∵CD是∠ACE的平分线,
∴∠DCE=70°.
∴∠D=40°
(2)∠A=2∠D.
证明:∵CD 平分∠ACE
∴∠ACE=2∠DCE
又∠DCE=∠D+∠DBC
∴2∠DCE=2∠D+2∠DBC
∵BD平分∠ABC
∴∠ABC=2∠DBC
即∠ACE=2∠D+∠ABC
而∠ACE=∠A+∠ABC
∴2∠D=∠A
-
科目: 来源: 题型:
查看答案和解析>>【题目】若ax﹣3b3与﹣3ab2y﹣1是同类项,则xy= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形两边长为3、6, 这个三角形周长为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】使用计算器计算各式:6×7= ,66×67= ,666×667= ,6 666×6 667= .
(1)根据以上结果,你发现了什么规律?
(2)依照你发现的规律,不用计算器,你能直接写出666 666×666 667的结果吗?请你试一试.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,
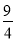 ),点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.(1)求该抛物线的函数关系表达式.
(2)点F为线段AC上一动点,过F作FE⊥x轴,FG⊥y轴,垂足分别为E、G,当四边形OEFG为正方形时,求出F点的坐标.
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在请说明理由.

-
科目: 来源: 题型:
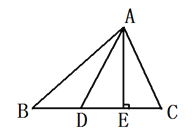
查看答案和解析>>【题目】(7分)如图,已知AE⊥BC,AD平分∠BAE,∠ADB=110°,∠CAE=20°.求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2x2 - 4x+c经过点(2, -3),则c的值为( )
A.-1B.2C.-3D.-2
相关试题

