【题目】已知:如图,AB为⊙ O的直径,点C、D在⊙ O上,且BC=6cm,AC=8cm,∠ABD=45°.
(1)求弧BD的长;
(2)求图中阴影部分的面积.

参考答案:
【答案】(1)![]() cm;(2)
cm;(2)![]() cm2.
cm2.
【解析】试题分析:(1)由AB为⊙O的直径,得到∠ACB=90°,由勾股定理求得AB,OB=5cm.连OD,得到等腰直角三角形,根据勾股定理即可得到结论;
(2)根据S阴影=S扇形-S△OBD即可得到结论.
试题解析:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∵BC=6cm,AC=8cm,
∴AB=10cm.
∴OB=5cm.
连OD,
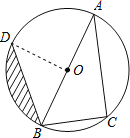
∵OD=OB,
∴∠ODB=∠ABD=45°.
∴∠BOD=90°.
∴BD=![]() cm.
cm.
(2)S阴影=S扇形-S△OBD=![]() π52-
π52-![]() ×5×5=
×5×5=![]() cm2.
cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法按要求对0.0603分别取近似值,其中错误的是( )
A.0.1 (精确到0.1)B.0.060(精确到0.001)
C.0.06(精确到百分位)D.0.06 (精确到十分位)
-
科目: 来源: 题型:
查看答案和解析>>【题目】买一个足球需要m元,买一个篮球需要n元,则买4个足球和7个篮球共需要多少元( )
A.4m+7nB.28mnC.7m+4nD.11mn
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A = 50°35',则∠A的余角是_____.
-
科目: 来源: 题型:
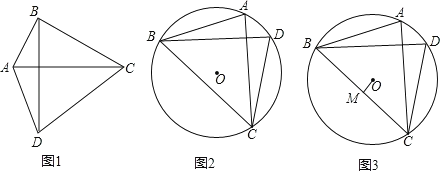
查看答案和解析>>【题目】若一个四边形的两条对角线互相垂直且相等,则称这个四边形为“奇妙四边形”.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据“奇妙四边形”对角线互相垂直的特征可得“奇妙四边形”的一个重要性质:“奇妙四边形”的面积等于两条对角线乘积的一半.根据以上信息回答:
(1)矩形 “奇妙四边形”(填“是”或“不是”);
(2)如图2,已知⊙O的内接四边形ABCD是“奇妙四边形”,若⊙O的半径为6,∠BCD=60°.求“奇妙四边形”ABCD的面积;
(3)如图3,已知⊙O的内接四边形ABCD是“奇妙四边形”作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D,E分别在边BC 和AC上,若AD=AE,则下列结论错误的是( )

A.∠ADB=∠ACB+∠CAD B.∠ADE=∠AED
C.∠CDE=
 ∠BAD D.∠AED=2∠ECD
∠BAD D.∠AED=2∠ECD -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点D在AB的延长线上.
(1)已知a=1,点B的纵坐标为2.
①如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,求AC的长.
②如图2,若BD=
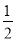 AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.
AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.(2)如图3,若BD=AB,过O,B,D三点的抛物线L3,顶点为P,对应函数的二次项系数为a3,过点P作PE∥x轴,交抛物线L于E,F两点,求
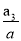 的值,并直接写出
的值,并直接写出 的值.
的值.
相关试题

