搜索
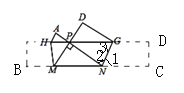
【题目】将长方形纸片ABCD如图折叠，B、C 两点恰好重合落在AD 边上的同一点P 处，折痕分别是MH、NG，已知∠MPN=90°，且PM=3，MN=5.则△PGN面积为____.
参考答案：
【答案】4.8.
【解析】
根据折叠性质得BM=PM，CN=PN；∠2=∠1,得∠2=∠3，PG=PN,根据勾股定理求出PN，再根据面积公式求h=
，再求面积.
将矩形纸片ABCD折叠，B、C两点恰好重合落在AD边上点P处，BM=PM，CN=PN；已知
，PM=3，MN=5,在
中由勾股定理得
，根据直角三角形的面积公式，在中
，解得h=，由AD∥BC,得∠3=∠1,又∠2=∠1,所以∠2=∠3，所以，PG=PN=4,所以，△PGN面积为4ⅹ
=4.8.
故答案为：4.8
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等腰
中，
，点A、B分别在坐标轴上.
（1）如图①，若
，
，求C点的坐标；（2）如图②，若点A的坐标为
，点B在y轴的正半轴上运动时，分别以OB，AB为边在第一，第二象限作等腰
，等腰
，连接EF交y轴于P点，当点B在y轴上移动时，PB的长度是否变化？如果不变求出PB值，如果变化求PB的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】直角坐标系中，已知A（1，0），以点A为圆心画圆，点M（4，4）在⊙A上，直线y=﹣
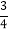x+b过点M，分别交x轴、y轴于B、C两点．（1）①填空：⊙A的半径为 ，b= ．（不需写解答过程）
②判断直线BC与⊙A的位置关系，并说明理由．
（2）若EF切⊙A于点F分别交AB和BC于G、E，且FE⊥BC，求
的值．（3）若点P在⊙A上，点Q是y轴上一点且在点C下方，当△PQM为等腰直角三角形时，直接写出点Q的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题：①如果3、4、5为一组勾股数，那么3k、4k、5k仍是勾股数；②含有45°角的直角三角形的三边长之比是1∶1:
；③如果一个三角形的三边是9，12，13，那么此三角形是直角三角形；④一个直角三角形的两边长是3和4，它的斜边是5．其中正确的个数是 ( )A.1个B.2个C.3个D.4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，二次函数y＝ax2﹣2ax﹣3a（a＜0）的图象与x轴交于A、B两点（点A在点B的右侧），与y轴的正半轴交于点C，顶点为D．
（1）求顶点D的坐标（用含a的代数式表示）；
（2）若以AD为直径的圆经过点C．
①求抛物线的函数关系式；
②如图2，点E是y轴负半轴上一点，连接BE，将△OBE绕平面内某一点旋转180°，得到△PMN（点P、M、N分别和点O、B、E对应），并且点M、N都在抛物线上，作MF⊥x轴于点F，若线段MF：BF＝1：2，求点M、N的坐标；
③点Q在抛物线的对称轴上，以Q为圆心的圆过A、B两点，并且和直线CD相切，如图3，求点Q的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明调查了班级里20位同学本学期购买课外书的花费情况，并将结果绘制成了如图的统计图．在这20位同学中，本学期购买课外书的花费的众数和中位数分别是（ ）
A. 50，50 B. 50，30 C. 80，50 D. 30，50
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，已知∠BAC＝45°，AD⊥BC于D，分别以AB、AC为对称轴，画出△ABD、△ACD的轴对称图形，D点的对称点为E、F，延长EB、FC相交于G点，得到正方形AEGF(AE＝EG＝GF＝AF,
∠EAF＝∠E＝∠F＝∠G=90°)．
(1) 若AD＝6，BD＝2，求CG的长．
(2) 设BG＝a,CG＝b,BC＝c.
①AE=_______.(用a、b、c表示)
②利用正方形面积验证勾股定理
．
相关试题
