【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,且∠BON=55°,求∠BOD的度数. 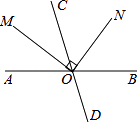
参考答案:
【答案】解:∵ON⊥OM, ∴∠MON=90°,
∵∠BON=55°,
∴∠AOM=180°﹣90°﹣55°=35°,
∵射线OM平分∠AOC,
∴∠AOC=2∠AOM=70°,
∴∠BOD=∠AOC=70°.
【解析】首先根据垂线的定义和已知条件求出∠AOM的度数,根据角平分线的定义求出∠AOC的度数,根据对顶角相等的性质即可得出所求.
【考点精析】根据题目的已知条件,利用角的平分线和对顶角和邻补角的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市对居民天然气收费采用阶梯气价,以“年度”作为一个阶梯气价结算周期,年度用气量分档和价格如下:第一档:年用气量0~242(含)立方米,价格a元/立方米,第二档:年用气量242~360(含)立方米,价格b元/立方米,即年用气量超过242度,超出部分气价按b元收费,某户居民一年用天然气300立方米,该户居民这一年应交纳天然气费是_____元.(用含a,b的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明(在括号中填写推理理由) 如图,
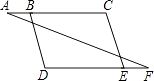
已知∠A=∠F,∠C=∠D,求证:BD∥CE.
证明:因为∠A=∠F,
所以AC∥DF(),
所以∠C+∠=180°().
因为∠C=∠D,
所以∠D+∠=180°(),
所以BD∥CE(). -
科目: 来源: 题型:
查看答案和解析>>【题目】随着移动互联网的快速发展,共享单车在余姚的大街小巷随处看见,解决了很多人的交通出行问题,李老师早上骑单车上班,中途因道路施工推车步行了一段路,到学校共用时15分钟,如果他骑单车的平均速度是每分钟250米,推车步行的平均速度是每分钟80米,他家离学校的路程是2900米,求他推车步行了多少分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a<-2,则-2a________4.
-
科目: 来源: 题型:
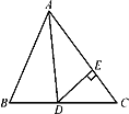
查看答案和解析>>【题目】如图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
相关试题

