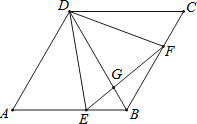
【题目】如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,BC上,EF与BD交于G,且∠DEF=60°,若AD=3,AE=2,则sin∠BEF= .
参考答案:
【答案】![]()
【解析】
试题分析:作EH⊥AD于H,由含30°角的直角三角形的性质得出AH,求出DH,由勾股定理EH,由勾股定理求出DE,由三角形的外角性质得出∠BEF=∠ADE,求出sin∠ADE即可.
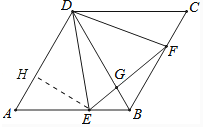
解:作EH⊥AD于H,如图所示:
则∠AEH=90°﹣∠A=30°,
∴AH=![]() AE=1,
AE=1,
∴EH=![]() =
=![]() ,
,
∵AD=3,
∴DH=AD﹣AH=2,
在Rt△DEH中,根据勾股定理得,DE=![]() =
=![]() ,
,
∵∠DEF+∠BEF=∠A+∠ADE,∠DEF=60°=∠A,
∴∠BEF=∠ADE,
∴sin∠BEF=sin∠ADE=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年我市财政收入451亿元,请使用科学记数法表示451亿元为元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设四边形的内角和等于a,六边形的外角和等于b,则a与b的关系是( )
A. a>b B. a<b C. a=b D. b=a+360°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段,能组成三角形的是( )
A. 4cm,5cm,9cm B. 5cm,5cm,10cm
C. 8cm,8cm,15cm D. 6cm,7cm,14cm
-
科目: 来源: 题型:
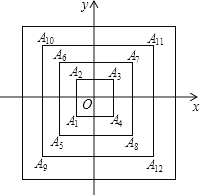
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2018的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数为( )
①无限小数都是无理数;②不循环小数都是无理数;③无理数都是无限小数;④无理数也有负数;⑤无理数分为正无理数、零、负无理数.
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

