【题目】如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边Ac沿CE翻折,使点A落在AB上的D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点F处,两条折痕与斜边AB分别交于点E、F,则线段BF的长为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解:根据折叠的性质可知CD=AC=3,B′C=BC=4,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB,
∴B′D=4﹣3=1,∠DCE+∠B′CF=∠ACE+∠BCF,
∵∠ACB=90°,
∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B′FC=135°,
∴∠B′FD=90°,
∵S△ABC= ![]() AC×BC=
AC×BC= ![]() AB×CE,
AB×CE,
∴AC×BC=AB×CE,
∵根据勾股定理求得AB=5,
∴CE= ![]() ,
,
∴EF= ![]() ,ED=AE=
,ED=AE= ![]() ,
,
∴DF=EF﹣ED= ![]() ,
,
∴B′F= ![]() .
.
∴BF=B'F= ![]() ,
,
所以答案是:B.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式4x4+1加上一个含字母的单项式,就能变形为一个含x的多项式的平方,则这样的单项式为 ___________ .
-
科目: 来源: 题型:
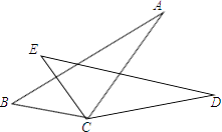
查看答案和解析>>【题目】如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
A.AB=DE
B.∠B=∠E
C.AC=DC
D.∠A=∠D -
科目: 来源: 题型:
查看答案和解析>>【题目】若2m-4与3m-1是同一个数的两个不等的平方根,则这个数是( )
A. 2B. 一2C. 4D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一个正数的两个平方根分别是-5和a+1,则a的值是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品涨价30%后欲恢复原价,则必须下降的百分数约为( )
A.20%
B.21%
C.22%
D.23% -
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+mx+16=(x+4)2,则m的值为__________.
相关试题

