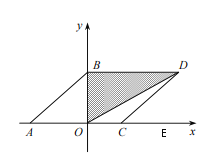
【题目】如图，在平面直角坐标系中，已知，两点，且、满足，点是射线上的动点（不与，重合），将线段平移到，使点与点对应，点与点对应，连接，.

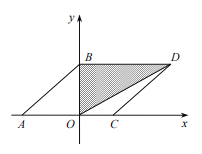
（1）求出点和点的坐标；

（2）设三角形面积为，若，求的取值范围；

（3）设，，，请给出，，满足的数量关系式，并说明理由.

【答案】（1）A（4，0），B（0，3）；（2）且m≠0；（3）=+，理由见解析

【解析】

（1）由算术平方根和绝对值的非负性质得出，即可求出a,b的值

，即可得出答案；

（2）根据三角形面积为==，再根据即可得到不等式组，即可求解；

（3）先根据平行的性质得到,再根据三角形的外角定理即可求解.

（1）∵m，n满足

∴

解得：

∴A（4，0），B（0，3）；

（2）∵点是射线上的动点（不与，重合），将线段平移到，使点与点对应，点与点对应，连接，.

∴四边形ACDB为平行四边形，

∴===

∵

∴

解得-

∵，点是射线上的动点（不与，重合），

∴且m≠0；

（3）=+，理由如下：

如图，∵AB∥CD，

∴=，

∵

∴+==

即=+.

关闭