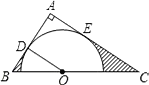
【题目】如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.
求:(1)tanC;
(2)图中两部分阴影面积的和.
参考答案:
【答案】解:(1)连接OE,
∵AB、AC分别切⊙O于D、E两点,
∴∠ADO=∠AEO=90°,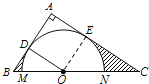
又∵∠A=90°,
∴四边形ADOE是矩形,
∵OD=OE,
∴四边形ADOE是正方形,
∴OD∥AC,OD=AD=3,
∴∠BOD=∠C,
∴在Rt△BOD中,![]() ,
,
∴![]() .
.
答:tanC=![]() .
.
(2)解:如图,设⊙O与BC交于M、N两点,
由(1)得:四边形ADOE是正方形,
∴∠DOE=90°,
∴∠COE+∠BOD=90°,
∵在Rt△EOC中,![]() ,OE=3,
,OE=3,
∴![]() ,
,
∴S扇形DOM+S扇形EON=S扇形DOE=![]() ,
,
∴S阴影=S△BOD+S△COE﹣(S扇形DOM+S扇形EON)=![]() ,
,
答:图中两部分阴影面积的和为![]() .
.
【解析】解:(1)连接![]()
∵![]() 、
、![]() 分别切
分别切![]() 于
于![]() 、
、![]() 两点
两点
∴![]()
又∵![]()
∴四边形![]() 是矩形
是矩形
∵![]()
∴四边形![]() 是正方形. .................................(2分)
是正方形. .................................(2分)
∴![]() ∥
∥![]() ,
, ![]()
∴![]()
∴在![]() 中,
中, ![]()
∴![]() . .................................(5分)
. .................................(5分)
(2)如图,设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点.由(1)得,四边形
两点.由(1)得,四边形![]() 是正方形
是正方形

∴![]()
∴![]()
∵在![]() 中,
中, ![]() ,
, ![]()
∴![]() . .................................(7分)
. .................................(7分)
∴![]()
∴![]()
∴图中两部分阴影面积的和为![]() ............ 9分
............ 9分
(1)连接![]() ,求得四边形
,求得四边形![]() 是正方形,得出AD的长,从而求得
是正方形,得出AD的长,从而求得![]()
(2)根据阴影面积等于三角形的面积减去扇形的面积求得
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
老舍先生曾说“天堂是什么样子,我不晓得,但从我的生活经验去判断,北平之秋便是天堂.”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少.
小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树.他先让爸爸开车驶过这段公路,发现速度为60千米/小时,走了约3分钟,由此估算这段路长约千米.
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米.小宇计划从路的起点开始,每a米种一棵树,绘制示意图如下:
考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵树,请你求出a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:
(1)非等边的等腰三角形有条对称轴,非正方形的长方形有条对称轴,等边三角形有条对称轴;
(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1﹣2和图1﹣3都可以看作由图1﹣1修改得到的,仿照类似的修改方式,请你在图1﹣4和图1﹣5中,分别修改图1﹣2和图1﹣3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;
(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;
(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.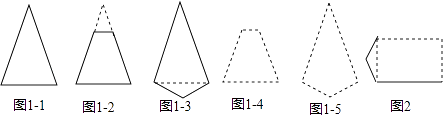
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】2x3y2与12x4y的公因式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家游泳中心﹣﹣“水立方”是北京2008年奥运会场馆之一,它的外层膜的展开面积约为260 000平方米,将260 000用科学记数法表示应为( )
A.0.26×106
B.26×104
C.2.6×106
D.2.6×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB垂直于弦CD,垂足为点E,过点C作⊙O 的切线,交AB的延长线于点P,联结PD.
(1)判断直线PD与⊙O的位置关系,并加以证明;
(2)联结CO并延长交⊙O于点F,联结FP交CD于点G,如果CF=10,cos∠APC=
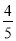 ,求EG的长.
,求EG的长.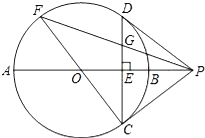
相关试题

