【题目】(1)如图1,直线AB,CD相交于点O,OE⊥AB,OF⊥CD.
①直接写出图中∠AOF的余角;
②如果∠EOF=![]() ∠AOD,求∠EOF的度数.
∠AOD,求∠EOF的度数.
(2)如图2,已知O为线段AB中点,AC=![]() AB,BD=
AB,BD=![]() AB,线段OC长为1,求线段AB,CD的长.
AB,线段OC长为1,求线段AB,CD的长.

参考答案:
【答案】(1)①∠AOF的余角为∠AOC,∠FOE,∠BOD;②30°(2)![]()
【解析】分析:(1)①由垂直的定义可知∠AOF+∠COA=90°,∠AOF+∠FOE=90°,从而可知∠COA与∠FOE是∠AOF的余角,由对顶角的性质从而的得到∠BOD是∠AOF的余角;②依据同角的余角相等可知∠FOE=∠DOB,∠EOF=![]() ∠AOD,从而得到∠EOF=
∠AOD,从而得到∠EOF=![]() 平角.(2)先根据中点的定义和已知得到OC所占的分率,从而得到线段AB的长,再根据已知得到CD所占的分率,从而得到线段CD的长.
平角.(2)先根据中点的定义和已知得到OC所占的分率,从而得到线段AB的长,再根据已知得到CD所占的分率,从而得到线段CD的长.
本题解析:
(1)①∵OE⊥AB,OF⊥CD,
∴∠AOF+∠COA=90°,∠AOF+∠FOE=90°.
∴∠COA与∠FOE是∠AOF的余角.
∵由对顶角相等可知:∠AOC=∠BOD,
∴∠BOD+∠AOF=90°.
∴∠BOD与∠APF互为余角.
∴∠AOF的余角为∠AOC,∠FOE,∠BOD;
②∵∠AOC=∠EOF,∠AOC+∠AOD=180°,∠EOF=![]() ∠AOD,
∠AOD,
∴6∠AOC=180°.
∴∠EOF=∠AOC=30°.
(2)∵O为线段AB中点,
∴AO=![]() AB,
AB,
∵AC=![]() AB,
AB,
∴OC=![]() AB,
AB,
∵线段OC长为1,
∴AB=6,
∵AC=![]() AB,BD=
AB,BD=![]() AB,
AB,
∴CD=AC+BD﹣AB=![]() AB=
AB=![]() ×6=
×6=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若现有长为3cm,4cm,7cm,9cm的四根木棒,任取其中三根组成一个三角形,则可以组成不同的三角形的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】5月14﹣15日“一带一路”论坛峰会在北京隆重召开,促进了我国与世界各国的互联互通互惠,“一带一路”地区覆盖总人数约为44亿人,44亿这个数用科学记数法表示为( )
A.4.4×108
B.4.4×109
C.4×109
D.44×108 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是甲、乙、丙三人百米赛跑的函数图象,根据右图回答下面问题;

(1)在这次比赛中,获得冠军:
(2)甲比乙提前秒到达目的地;
(3)乙的速度比丙快米/秒. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是假命题的是( )
A.两点之间,线段最短B.同旁内角互补
C.直角的补角仍然是直角D.垂线段最短
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2+bx+c与x轴交于A(1,0),B(m,0),与y轴交于C.
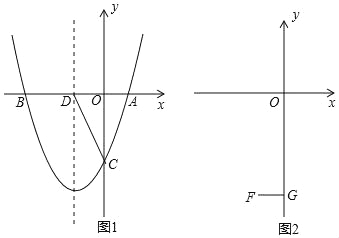
(1)若m=﹣3,求抛物线的解析式,并写出抛物线的对称轴;
(2)如图1,在(1)的条件下,设抛物线的对称轴交x轴于D,在对称轴左侧的抛物线上有一点E,使S△ACE=
 S△ACD,求点E的坐标;
S△ACD,求点E的坐标;(3)如图2,设F(﹣1,﹣4),FG⊥y于G,在线段OG上是否存在点P,使∠OBP=∠FPG?若存在,求m的取值范围;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】会议室2排3号记作(2,3),那么3排2号记作( )
A.(3,2)B.(2,3)C.(-3,-2)D.(-2,-3)
相关试题

