【题目】已知a,b,c分别是△ABC的三边,当m>0时,关于x的一元二次方程c(x2+m)+b(x2-m)-2![]() ax=0有两个相等的实数根,试判断△ABC的形状,并说明理由.
ax=0有两个相等的实数根,试判断△ABC的形状,并说明理由.
参考答案:
【答案】△ABC是直角三角形.理由见解析.
【解析】【试题分析】根据一元二次方程有两个相等的实数根,判断![]() =0,即Δ=4ma2-4m(c-b)(c+b)=4m(a2+b2-c2)=0, 即a2+b2-c2=0,即a2+b2=c2,根据勾股定理的逆定理,得到△ABC是直角三角形.
=0,即Δ=4ma2-4m(c-b)(c+b)=4m(a2+b2-c2)=0, 即a2+b2-c2=0,即a2+b2=c2,根据勾股定理的逆定理,得到△ABC是直角三角形.
【试题解析】
△ABC是直角三角形.理由如下:
原方程可化为(b+c)x2-2 ![]() ax+cm-bm=0,
ax+cm-bm=0,
Δ=4ma2-4m(c-b)(c+b)=4m(a2+b2-c2).
∵m>0,且原方程有两个相等的实数根,
∴a2+b2-c2=0,即a2+b2=c2.
∴△ABC是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论:①∠BOE=
 (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论(填编号). 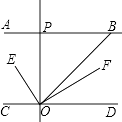
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5=180°,其中正确的个数是( )
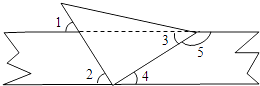
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三边a,b,c中,a=b-1,c=b+1,又已知关于x的方程4x2-20x+b+12=0的根恰为b的值,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足
 ,过C作CB⊥x轴于B.
,过C作CB⊥x轴于B.
(1)求△ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得△ABC和△ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中结果为负数的是( )
A. ﹣(﹣2) B. (﹣2)2 C. ﹣|﹣2| D. |﹣2|
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.

(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值
相关试题

