搜索
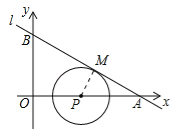
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：
与x轴、y轴分别交于A、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（ ）
A．6 B．8 C．10 D．12
参考答案：
【答案】A．
【解析】
试题分析：∵直线l：
与x轴、y轴分别交于A、B，∴B（0，
），∴OB=
，在RT△AOB中，∠OAB=30°，∴OA=
OB=
=12，∵⊙P与l相切，设切点为M，连接PM，则PM⊥AB，∴PM=
PA，设P（x，0），∴PA=12﹣x，∴⊙P的半径PM=PA=
，∵x为整数，PM为整数，∴x可以取0，2，4，6，8，10，共6个数，∴使得⊙P成为整圆的点P个数是6．故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平行四边形ABCD中，∠B+∠D=200°，则∠A的度数为____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】请你写出一个绝对值小于3.7的负数，你写的是____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图，在平面直角坐标系xOy中，点A、B、C分别为坐标轴上上的三个点，且OA=1，OB=3，OC=4．
（1）求经过A、B、C三点的抛物线的解析式；
（2）在平面直角坐标系xOy中是否存在一点P，使得以以点A、B、C、P为顶点的四边形为菱形？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）若点M为该抛物线上一动点，在（2）的条件下，请求出当|PM﹣AM|的最大值时点M的坐标，并直接写出|PM﹣AM|的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB与CD相交于点O，OP是∠BOC的平分线，OE⊥AB，OF⊥CD，
（1）图中除直角外，还有相等的角吗？请写出两对：①；② ．
（2）如果∠AOD＝40°，则①∠BOC＝；②OP是∠BOC的平分线，所以∠COP＝；
③求∠BOF的度数 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如果|a+3|+(b-2)2=0，那么代数式(a+b)2019的值为____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】9的算术平方根是( )
A. 3 B. 9 C. ±3 D. ±9
相关试题
