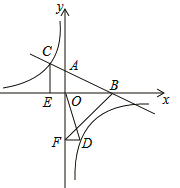
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果S△BAF=4S△DFO,求点D的坐标.
参考答案:
【答案】(1)y=-![]() ;(2)D(
;(2)D(![]() ,一4).
,一4).
【解析】
试题分析:(1)先由tan∠ABO=![]() =
=![]() 及OB=4,OE=2求出CE的长度,从而得到点C的坐标,再将点C的坐标代入y=
及OB=4,OE=2求出CE的长度,从而得到点C的坐标,再将点C的坐标代入y=![]() 即可求得反比例函数的解析式.(2)先由反比例函数y=
即可求得反比例函数的解析式.(2)先由反比例函数y=![]() 的k的几何意义得出S△DFO,由S△BAF=4S△DFO得到S△BAF,根据S△BAF=
的k的几何意义得出S△DFO,由S△BAF=4S△DFO得到S△BAF,根据S△BAF=![]() AFOB得出AF的长度,用AF-OA求出OF的长,据此可先得出点D的纵坐标,再求D得横坐标.
AFOB得出AF的长度,用AF-OA求出OF的长,据此可先得出点D的纵坐标,再求D得横坐标.
试题解析:(l)∵OB=4,OE=2,∴BE=OB+OE=6.
∵CE⊥x轴,∴∠CEB=90°.
在Rt△BEC中,∵tan∠ABO=![]() ,∴
,∴![]() =
=![]() .即
.即![]() =
=![]() ,解得CE=3.
,解得CE=3.
结合图象可知C点的坐标为(一2,3),
将C(―2,3)代入反比例函数解析式可得3=![]() .解得m=-6.
.解得m=-6.
反比例函数解析式为y=-![]() .
.
(2)解:方法一:∵点D是y=-![]() 的图象上的点,且DF⊥y轴,
的图象上的点,且DF⊥y轴,
∴S△DFO=![]() ×|-6|=3.
×|-6|=3.
∴S△BAF=4S△DFO=4×3=12.∴![]() AFOB=12.∴
AFOB=12.∴![]() ×AF×4=12.
×AF×4=12.
∴AF=6.∴EF=AF-OA=6-2=4.
∴点D的纵坐标为-4.
把y=-4代入y=-![]() ,得 -4=-
,得 -4=-![]() .∴x=
.∴x=![]() .
.
∴D(![]() ,一4).
,一4).
方法二:设点D的坐标为(a,b).
∵S△BAF=4S△DFO,∴![]() AFOB=4×
AFOB=4×![]() OFFD.∴(AO+OF) OB=4OFFD.
OFFD.∴(AO+OF) OB=4OFFD.
∴[2+(-b)]×4=-4ab.∴8-4b=-4ab.
又∵点D在反比例函数图象上,∴b=-![]() .∴ab=-6.∴8-4b=24.解得:b=-4.
.∴ab=-6.∴8-4b=24.解得:b=-4.
把b=-4代ab=-6中,解得:a=![]() .
.
∴D(![]() ,一4).
,一4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x-2y=4,用关于y的代数式表示x,则x=____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解1000个箱子的质量情况,从中随机抽取50个箱子进行检查,则抽样( )
A. 不够合理,容量太小B. 不够合理,不具有代表性
C. 不够合理,遗漏了950个箱子D. 合理、科学
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.

(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF,OD,OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F=
 ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2﹣8x﹣9=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个矩形的面积为a2+2a,若一边长为a,则另一边长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某厂生产的2000台冰箱的质量情况,把这2000台冰箱编上序号,然后用抽签的方法抽取100台,这种抽样方法是________,这种抽样方法______(填“具有”或“不具有”)代表性.
相关试题

