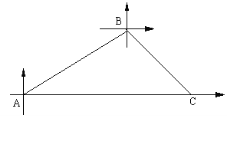
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会和,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求港口A与小岛C之间的距离.
参考答案:
【答案】(![]() )海里
)海里
【解析】
试题分析:作BD⊥AC于点D,根据题意得出AB=30,∠BAC=30°,∠BCA=45°,根据Rt△ABD的三角函数得出BD的长度,然后根据Rt△BCD的三角函数得出CD的长度,最后根据AD+CD=AC得出答案.
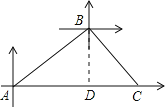
试题解析:作BD⊥AC于点D,如图所示:由题意可知:AB=30×1=30,∠BAC=30°,∠BCA=45°,
在Rt△ABD中, ∵AB=30,∠BAC=30°, ∴BD=15,AD=ABcos30°=![]() ,
,
在Rt△BCD中, ∵BD=15,∠BCD=45°, ∴CD=15海里, ∴AC=AD+CD=![]() ,
,
即A、C间的距离为(![]() )海里.
)海里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值。如对于任意正实数
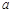 、x,可作变形:x+=(-
、x,可作变形:x+=(-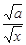 )2+2,因为(-
)2+2,因为(-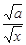 )2≥0,所以x+≥2(当x=时取等号).
)2≥0,所以x+≥2(当x=时取等号).记函数y=x+(a>0,x>0),由上述结论可知:当x=时,该函数有最小值为2.
直接应用: 已知函数y1=x(x>0)与函数y2 = (x>0),则当x= 时,y1+y2取得最小值为 .
变形应用: 已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),求 的最小值,并指出取得该最小值时相应的x的值.
实际应用:汽车的经济时速是指汽车最省油的行驶速度。某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油(+)升。若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
①、求y关于x的函数关系式(写出自变量x的取值范围);
②、求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
-
科目: 来源: 题型:
查看答案和解析>>【题目】四川512大地震中,一批灾民要住进“过渡安置”房,如果每个房间住3人,则多8人,如果每个房间住5人,则有一个房间不足5人,问这次为灾民安置的有多少个房间?这批灾民有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查某市中小学生对“营养午餐”的满意程度,适合采用的调查方式是 . (填“全面调查”或“抽样调查”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数据中,能构成三角形的是( )
A. 1、2、3 B. 2、3、4 C. 4、9、4 D. 2、1、4
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们学校教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:30)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
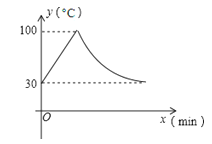
A.7:00 B.7:05 C.7:10 D.7:15
相关试题

