【题目】如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 .
参考答案:
【答案】![]() ≤a≤
≤a≤![]() .
.
【解析】
试题因为AC为对角线,故当AC最小时,正方形边长此时最小.
①当A、C都在对边中点时(如下图所示位置时),显然AC取得最小值,
∵正六边形的边长为1,
∴AC=![]() ,
,
∴a2+a2=AC2=![]() .
.
∴a=![]() =
=![]() .
.
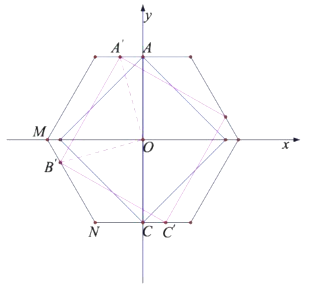
②当正方形四个顶点都在正六边形的边上时,a最大(如下图所示).
设A′(t,![]() )时,正方形边长最大.
)时,正方形边长最大.
∵OB′⊥OA′.
∴B′(-![]() ,t)
,t)
设直线MN解析式为:y=kx+b,M(-1,0),N(-![]() ,-
,-![]() )(如下图)
)(如下图)
∴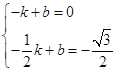 .
.
∴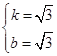 .
.
∴直线MN的解析式为:y=![]() (x+1),
(x+1),
将B′(-![]() ,t)代入得:t=
,t)代入得:t=![]() -
-![]() .
.
此时正方形边长为A′B′取最大.
∴a=![]() =3-
=3-![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年中秋节来期间,某超市以每盒80元的价格购进了1000盒月饼,第一周以每盒168元的价格销售了300盒,第二周如果单价不变,预计仍可售出300盒,该超市经理为了增加销量,决定降价,据调查,单价每降低1元,可多售出10盒,但最低每盒要赢利30元,第二周结束后,该超市将对剩余的月饼一次性赔钱甩卖,此时价格为70元/盒.
(1)若设第二周单价降低x元,则第二周的单价是 ______ ,销量是 ______ ;
(2)经两周后还剩余月饼 ______ 盒;
(3)若该超市想通过销售这批月饼获利51360元,那么第二周的单价应是多元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如
 .善于思考的小明进行了以下探索:
.善于思考的小明进行了以下探索:设
 (其中
(其中 、
、 、
、 、
、 均为整数),则有
均为整数),则有 .
.∴
 ,
, .这样小明就找到了一种把类似
.这样小明就找到了一种把类似 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法解决下列问题:
(1)当
 、
、 、
、 、
、 均为正整数时,若
均为正整数时,若 ,用含
,用含 、
、 的式子分别表示
的式子分别表示 、
、 ,得
,得 _________,
_________, _________.
_________.(2)利用所探索的结论,填空:
 (_____+_____
(_____+_____ )2;
)2;(3)若
 ,且
,且 、
、 、
、 均为正整数,求
均为正整数,求 的值?
的值? -
科目: 来源: 题型:
查看答案和解析>>【题目】(2017四川省达州市,第16题,3分)如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=
 ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=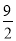 CE;④
CE;④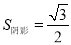 .其中正确结论的序号是__________.
.其中正确结论的序号是__________.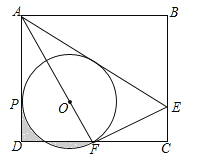
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,
 点坐标
点坐标 ,且
,且 ,
, 满足
满足

(1)如图(1)当
 为等腰直角三角形时;
为等腰直角三角形时;①点
 坐标为__________;点
坐标为__________;点 坐标为__________.
坐标为__________.②在(1)的条件下,分别以
 和
和 为边作等边
为边作等边 和等边
和等边 ,连结
,连结 ,求
,求 的度数.
的度数.(2)如图(2),过点
 作
作 轴于点
轴于点 ,点
,点 为
为 轴正半轴上一点,
轴正半轴上一点, 为
为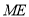 延长线上一点,以
延长线上一点,以 为直角边作等腰直角三角形
为直角边作等腰直角三角形 ,
, ,过点
,过点 作
作 轴交
轴交 于点
于点 ,连结
,连结 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,∠ABC=20°,外角∠ABF的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度.

A.4B.5C.6D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA.
(1)求证:∠BAD=∠EDC;
(2)作出点E关于直线BC的对称点M,连接DM、AM,猜想DM与AM的数量关系,并说明理由.

相关试题

