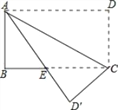
【题目】如图,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.
参考答案:
【答案】![]()
【解析】试题分析:根据矩形性质得AB=DC=6,BC=AD=8,AD∥BC,∠B=90°,再根据折叠性质得∠DAC=∠D′AC,而∠DAC=∠ACB,则∠D′AC=∠ACB,所以AE=EC,设BE=x,则EC=4-x,AE=4-x,然后在Rt△ABE中利用勾股定理可计算出BE的长即可.
试题解析:∵四边形ABCD为矩形,
∴AB=DC=3,BC=AD=4,AD∥BC,∠B=90°,
∵△ACD沿AC折叠到△ACD′,AD′与BC交于点E,
∴∠DAC=∠D′AC,
∵AD∥BC,∴∠DAC=∠ACB,
∴∠D′AC=∠ACB,∴AE=EC,
设BE=x,则EC=4﹣x,AE=4﹣x,
在Rt△ABE中,∵AB2+BE2=AE2,
∴32+x2=(4﹣x)2,解得x=![]() ,
,
即BE的长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】4的算术平方根是( )
A. -2B. 4C. 3D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B为单项式,且5x(A﹣2y)=30x2y3+B,则A= , B= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:15,16,14,16,17,16,15,则这组数据的中位数是( )
A. 17 B. 16 C. 15 D. 14
-
科目: 来源: 题型:
查看答案和解析>>【题目】某欢乐谷为回馈广大谷迷,在暑假期间推出学生个人门票优惠价,各票价如下:
票价种类
(A)学生夜场票
(B)学生日通票
(C)节假日通票
单价(元)
80
120
150
某慈善单位欲购买三种类型的票共100张奖励品学兼优的留守学生,其中购买的B种票数是A种票数的3倍还多7张,设购买A种票x张,C种票y张.
(1)直接写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W(元)与x(张)之间的函数关系式;
(3)为方便学生游玩,计划购买的学生夜场票不低于20张,且每种票至少购买5张,则有几种购票方案?并指出哪种方案费用最少. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校生物兴趣小组把一块沿河的三角形废地(如图)开辟为生物园(设AB段河岸为直线),已知∠ACB=90°,∠CAB=55°,BC=80米,学校决定在点C处建一个蓄水池,利用管道从河中取水,已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示实数
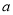 、
、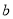 ,A、B两点之间的距离记作AB.
,A、B两点之间的距离记作AB.当A、B两点中有一点为原点时,不妨设A点在原点.如图①所示,则AB=OB=
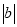 =
=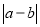 .
.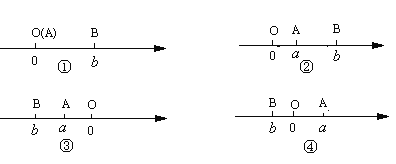
当A、B两点都不在原点时:
(1)如图②所示,点A、B都在原点的右边,不妨设点A在点B的左侧,则AB=OB-OA=
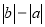 =
=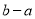 =
=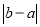 =
=
(2)如图③所示,点A、B都在原点的左边,不妨设点A在点B的右侧,则AB=OB-OA=
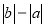 =
=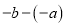 =
=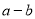 =
=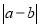
(3)如图④所示,点A、B分别在原点的两边,不妨设点A在点O的右侧,则AB=OB+OA=
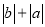 =
=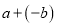 =
=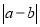
回答下列问题:
(1)综上所述,数轴上A、B两点之间的距离AB= .
(2)数轴上表示2和-4的两点A和B之间的距离AB= .
(3)数轴上表示
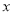 和-2的两点A和B之间的距离AB= ,如果AB=2,则
和-2的两点A和B之间的距离AB= ,如果AB=2,则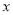 的值为 .
的值为 .(4)若代数式
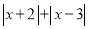 有最小值,则最小值为 .
有最小值,则最小值为 .
相关试题

