Question

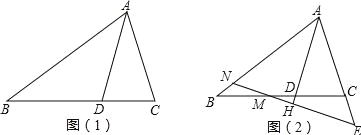
【题目】如图，在△ABC中，BA=BC，D在边CB上，且DB=DA=AC．

（1）如图1，填空∠B= °，∠C= °；

（2）若M为线段BC上的点，过M作直线MH⊥AD于H，分别交直线AB、AC与点N、E，如图2

①求证：△ANE是等腰三角形；

②试写出线段BN、CE、CD之间的数量关系，并加以证明．

Answer 1

【答案】(1)36 ；72 ；(2)①证明详见解析；②CD=BN+CE，理由详见解析.

【解析】

试题分析：（1）BA=BC，且DB=DA=AC可得∠C=∠ADC=∠BAC=2∠B，∠DAC=∠B，在△ADC中由三角形内角和可求得∠B，∠C；

（2）①由（1）可知∠BAD=∠CAD=36°，且∠AHN=∠AHE=90°，可求得∠ANH=∠AEH=54°，可得AN=AE；

②由①知AN=AE，借助已知利用线段的和差可得CD=BN+CE．

试题解析：（1）∵BA=BC，

∴∠BCA=∠BAC，

∵DA=DB，

∴∠BAD=∠B，

∵AD=AC，

∴∠ADC=∠C=∠BAC=2∠B，

∴∠DAC=∠B，

∵∠DAC+∠ADC+∠C=180°，

∴2∠B+2∠B+∠B=180°，

∴∠B=36°，∠C=2∠B=72°，

故答案为：36；72；

（2）①在△ADB中，∵DB=DA，∠B=36°，

∴∠BAD=36°，

在△ACD中，∵AD=AC，

∴∠ACD=∠ADC=72°，

∴∠CAD=36°，

∴∠BAD=∠CAD=36°，

∵MH⊥AD，

∴∠AHN=∠AHE=90°，

∴∠AEN=∠ANE=54°，

∴AN=AE，

即△ANE是等腰三角形；

②CD=BN+CE．

证明：由①知AN=AE，

又∵BA=BC，DB=AC，

∴BN=AB﹣AN=BC﹣AE，CE=AE﹣AC=AE﹣BD，

∴BN+CE=BC﹣BD=CD，

即CD=BN+CE．