【题目】重庆市的重大惠民工程﹣﹣公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=![]() x+5,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=-
x+5,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=-![]() x+
x+![]() (x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/m2)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:
(x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/m2)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:
z(元/m2) | 50 | 52 | 54 | 56 | 58 | … |
x(年) | 1 | 2 | 3 | 4 | 5 | … |
(1)求出z与x的函数关系式;
(2)求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
(3)若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高a%,这样可解决住房的人数将比第6年减少1.35a%,求a的值.
(参考数据:![]() ,
,![]() ,
,![]() )
)
参考答案:
【答案】(1)z=2x+48(2)第3年收取的租金最多,最多为243百万元(3)a的值为20
【解析】试题分析:(1)设z=kx+b(k≠0),然后把表格中的两组数据代入解析式,解方程组即可;(2)设收取的租金为W百万元,分别求出当1≤x≤6时和当7≤x≤10时的W与x的函数关系式,然后分别求出两个函数的最大值,比较大小,可确定收取的租金的最大值;(3)先求出第6年和第10年的投入使用的公租房面积,然后根据题意列方程得:20×(1-1.35a%)×20×(1+a%)=350,然后解方程即可.
试题解析:解:(1)由题意,z与x成一次函数关系,
设z=kx+b(k≠0).把(1,50).(2,52)代入,
得![]() ∴z=2x+48. (2分)
∴z=2x+48. (2分)
(2)当1≤x≤6时,设收取的租金为W1百万元,则
W1=(-![]() x+5)(2x+48)
x+5)(2x+48)
=-![]() x2+2x+240,
x2+2x+240,
∵对称轴x=-![]() ≠=3,而1≤x≤6,
≠=3,而1≤x≤6,
∴当x=3时,W1最大=243(百万元).
当7≤x≤10时,设收取的租金为W2百万元,则
W2=(-![]() x+
x+![]() )·(2x+48)
)·(2x+48)
=-![]() x2+
x2+![]() x+228.
x+228.
∵对称轴x=-![]() =7,而7≤x≤10,
=7,而7≤x≤10,
∴当x=7时,W2最大=![]() (百万元).
(百万元).
∵243>![]() ,
,
∴第3年收取的租金最多,最多为243百万元. (6分)
(3)当x=6时,
y=-![]() ×6+5=4百万平方米=400万平方米;
×6+5=4百万平方米=400万平方米;
当x=10时,
y=-![]() ×10+
×10+![]() =3.5百万平方米=350万平方.
=3.5百万平方米=350万平方.
∵第6年可解决20万人住房问题,
∴人均住房为400÷20=20平方米.
由题意20×(1-1.35a%)×20×(1+a%)=350.
设a%=m,化简为54m2+14m-5=0,
Δ=142-4×54×(-5)=1276,
∴m=![]()
∵![]() ≈17.8,∴m1=0.2,m2=-
≈17.8,∴m1=0.2,m2=-![]() (不符题意,舍去).
(不符题意,舍去).
∴a%=0.2,∴a=20.
答:a的值为20. (10分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的点A,O,B,C,D分别表示-3,0,2.5,5,-6.

(1)求B,O两点间的距离;
(2)求A,D两点间的距离;
(3)求C,B两点间的距离;
(4)请观察思考,若点A表示数m,且m<0,点B表示数n,且n>0,用含m,n的代数式表示A,B两点间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF⊥AD,将平行四边形ABCD沿着EF对折.设∠1的度数为n°,则∠C=______.(用含有n的代数式表示)

-
科目: 来源: 题型:
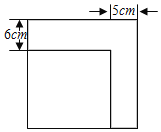
查看答案和解析>>【题目】如图,小刚将一个正方形纸片剪去一个宽为5cm的长条后,再从剩下的长方形纸片上剪去一个宽为6cm的长条.如果两次剪下的长条面积正好相等,求两个所剪下的长条的面积之和.
-
科目: 来源: 题型:
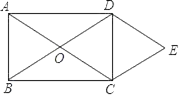
查看答案和解析>>【题目】如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若点E到CD的距离为2,CD=3,试求出矩形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶情况记录如下(单位:千米):+10,﹣8,+7,﹣15,+6,﹣16,+4,﹣2
(1)A处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油0.5升,这一天共耗油多少升?
-
科目: 来源: 题型:
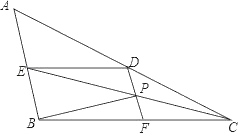
查看答案和解析>>【题目】如图,在△ABC中,CE平分∠ACB交AB于E点,DE∥BC,DF∥AB.
(1)若∠BCE=25°,请求出∠ADE的度数;
(2)已知:BF=2BE,DF交CE于P点,连结BP,AB⊥BP.
①猜想:△CDF的边DF与CD的数量关系,并说明理由;
②取DE的中点N,连结NP.求证:∠ENP=3∠DPN.
相关试题

