【题目】直线AB、CD相交于点O.
(1)OE、OF分别是∠AOC、∠BOD的平分线.画出这个图形.
(2)射线OE、OF在同一条直线上吗?(直接写出结论)
(3)画∠AOD的平分线OG.OE与OG有什么位置关系?并说明理由.
参考答案:
【答案】
(1)解:如图中红线所示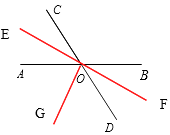
(2)解:∵ OE平分∠AOC ,OF平分∠BOD ,
∴ ∠COE=![]() ∠AOC ,∠DOF=
∠AOC ,∠DOF=![]() ∠BOD ,
∠BOD ,
∵ ∠AOC=∠BOD ,
∴ ∠EOC=∠DOF
,∵ ∠COE+∠EOD=180° ,
∴ ∠EOD+∠DOF=180° ,
即射线OE、OF在同一条直线上 。
(3)解:∵EF平分∠AOC和∠BOD,并且∠AOC=∠BOD,∴∠AOE=∠DOF.∵OG平分∠AOD,∴∠AOG=∠DOG.∵∠AOE+∠DOF+∠AOG+∠DOG=180°,∴∠DOF+∠DOG=180°÷2=90°,∴OE⊥OG
【解析】(1),用圆规在OA、OC上分别截取相等的线段,以与两边的交点为圆心,以大于![]() 交点间的距离的长为半径作弧,两弧在∠AOC内交于点E,作射线OE,则OE就是∠AOC的平分线,同理作出∠BOD的平分线;
交点间的距离的长为半径作弧,两弧在∠AOC内交于点E,作射线OE,则OE就是∠AOC的平分线,同理作出∠BOD的平分线;
(2),要判断射线OE,OF是否在同一直线上,只需判断∠EOD+∠DOF=180°是否成立,根据角平分线的性质可得 ∠COE=![]() ∠AOC ,∠DOF=
∠AOC ,∠DOF=![]() ∠BOD ,
∠BOD ,
再结合对顶角相等得, ∠EOC=∠DOF ,根据平角的定义得∠COE+∠EOD=180° , 从而得出 ∠EOD+∠DOF=180° ,即射线OE、OF在同一条直线上 ;
(3),根据角平分线的定义及对顶角相等得出∠AOE=∠DOF ,∠AOG=∠DOG ,根据平角的定义得出∠AOE+∠DOF+∠AOG+∠DOG=180° ,从而得出∠DOF+∠DOG=180°÷2=90°,即OE⊥OG 。
-
科目: 来源: 题型:
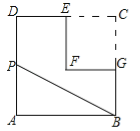
查看答案和解析>>【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A.
 B.
B. C.
C.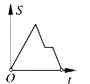 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解七年级同学每天的睡眠时间,在七年级的10个班中,每班抽5名学生做调查,这一调查中,总体是指_____,样本是指_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列描述一次函数y=-2x+5图象性质错误的是( )
(A)y随x的增大而减小
(B)直线经过第一、二、四象限
(C)直线从左到右是下降的
(D)直线与x轴交点坐标是(0,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E、F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( )

A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】平行线的性质:
性质1:两直线平行,同位角_____;
性质2:两直线____,内错角相等;
性质3:两直线平行,_____互补.
相关试题

