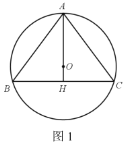
【题目】如图1，已知，⊙O是△ABC的外接圆，AB=AC=10，BC=12，连接AO并延长交BC于点H．

（1）求外接圆⊙O的半径；

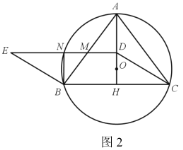
（2）如图2，点D是AH上（不与点A，H重合）的动点，以CD，CB为边，作平行四边形CDEB，DE分别交⊙O于点N，交AB边于点M．

①连接BN，当BN⊥DE时，求AM的值；

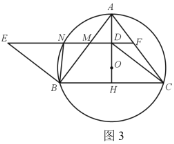
②如图3，延长ED交AC于点F，求证：NM·NF=AM·MB；

③设AM=x，要使-2<0成立，求x的取值范围．

【答案】（1）半径为；（2）①；②详见解析；③当时，有成立．

【解析】

（1）如下图，在Rt△ABH中，先求得AH的值，设OA=r，在Rt△OBH中，利用勾股定理可求得r的长；

（2）①如下图，在，可求得BN的长，然后在矩形NBHD中，求得AD的值，最后利用cos∠MAD求得AM；

②如下图，同过证可得结论；

③如下图，通过转换，先得出这个等式，然后利用，设AM=x，可得到关于x的方程，进而求出x的取值范围．

解：（1）如图1，连接，

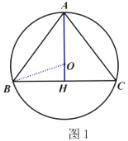
∵过圆心，∴，

∵，∴，

在中，，

设半径，则，在中，，

解得，即半径为．

（2）①如图2，连接

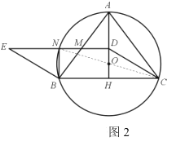
在平行四边形中，，∴．

∵，即，∴．

∴是的直径．．

∴在中，．

∵四边形CDEB是平行四边形，NB⊥BH，DH⊥BH

∴四边形是矩形，

∴，，∴．

∴在中，，∴，

②如图3，连接，，

∵，∴．

∵，∴．

由，可得，

∴，．

∴，．

∴，即．

③∵，，∴，∵，∴，

∴

．

∵，∴，

由，得，

∴．

该函数图象的示意图如图4

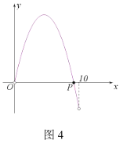
易求得点坐标为

∴当时，有成立．

关闭