【题目】如图,在矩形ABCD中,AD=6,AB=4,点E,G,H,F分别在AB,BC,CD,AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE,PF,PG,PH,则△PEF和△PGH的面积和等于 . 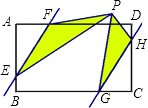
参考答案:
【答案】7
【解析】∵在矩形ABCD中,AD=6,AB=4,AF=CG=2,BE=DH=1,
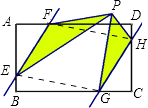
∴AE=AB﹣BE=4﹣1=3,
CH=CD﹣DH=4﹣1=3,
∴AE=CH,
在△AEF与△CGH中, 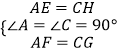 ,
,
∴△AEF≌△CGH(SAS),
∴EF=GH,
同理可得,△BGE≌△DFH,
∴EG=FH,
∴四边形EGHF是平行四边形,
∵△PEF和△PGH的高的和等于点H到直线EF的距离,
∴△PEF和△PGH的面积和= ![]() ×平行四边形EGHF的面积,
×平行四边形EGHF的面积,
∵平行四边形EGHF的面积
=4×6﹣ ![]() ×2×3﹣
×2×3﹣ ![]() ×1×(6﹣2)﹣
×1×(6﹣2)﹣ ![]() ×2×3﹣
×2×3﹣ ![]() ×1×(6﹣2),
×1×(6﹣2),
=24﹣3﹣2﹣3﹣2,
=14,
∴△PEF和△PGH的面积和= ![]() ×14=7.
×14=7.
故答案为:7.
由矩形性质得AD=6,AB=4,AF=CG=2,BE=DH=1,从而得出AE=CH;根据全等三角形的判定SAS可得△AEF≌△CGH,依据全等三角形的性质可得EF=GH;同理可得:△BGE≌△DFH,EG=FH,两组对边分别相等的四边形是平行四边形,由此得四边形EGHF是平行四边形,从而得出S△PEF+S△PGH=![]() S平行四边形EGHF,求出平行四边形EGHF的面积,即可得那两个三角形面积之和.
S平行四边形EGHF,求出平行四边形EGHF的面积,即可得那两个三角形面积之和.
-
科目: 来源: 题型:
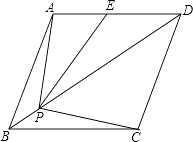
查看答案和解析>>【题目】如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( )
A.
B.2
C.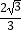
D.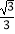
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
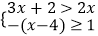 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.
B.
C.
D.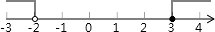
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织学生去福利院献爱心,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)向甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的总费用不超过2400元,那么最多可购买多少个甲礼品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处.
⑴若∠PEF=48°,点Q恰好落在其中的一条平行线上,则∠EFP的度数为 .
⑵若∠PEF=75°,∠CFQ=
 ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形如图2.
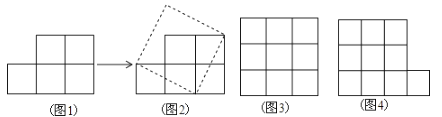
(1)你能在
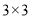 方格图(图3)中,连接四个格点(网格线的交点)组成面积为5的正方形吗?若能,请用虚线画出.
方格图(图3)中,连接四个格点(网格线的交点)组成面积为5的正方形吗?若能,请用虚线画出.(2)你能把十个小正方形组成的图形纸(图4),剪开并拼成正方形吗?若能,请仿照图2的形式把它重新拼成一个正方形.
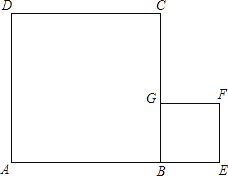
(3)如图,是由两个边长不等的正方形纸片组成的一个图形,要将其剪拼成一个既不重叠也无空隙的大正方形,则剪出的块数最少为________块.请你在图中画出裁剪线,并说明拼接方法.
相关试题

