【题目】如图,直线y=﹣3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x﹣2)2+k经过点A、B.求:
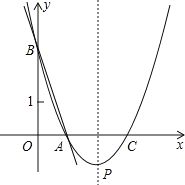
(1)点A、B的坐标;
(2)抛物线的函数表达式;
(3)在抛物线对称轴上是否存在点P,使得以A、B、P为顶点的三角形为等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)A(1,0)、B(0,3).(2)y=(x﹣2)2﹣1.(3)所求的点为P1(2,3),P2(2,3+![]() ),P3(2,3﹣
),P3(2,3﹣![]() ),P4(2,2).
),P4(2,2).
【解析】
试题分析:(1)由y=﹣3x+3得,当x=0时,y=3;当y=0时,x=1,即可确定点A,B的坐标;
(2)把点A(1,0)、B(0,3)代入y=a(x﹣2)2+k得: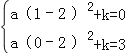 ,解得
,解得![]() ,即可解答;
,即可解答;
(3)存在,由AO=1,BO=3,得到AB=![]() .设对称x轴交于点D,P(2y),D(2,0),所以DA=1,PD=|y|,PA2=PD2+DA2=y2+1,分三种情况讨论解答:当PA=AB即PA2=AB2=10时;当PB=AB即PB2=AB2=10时;当PA=PB即PA2=PB2时.
.设对称x轴交于点D,P(2y),D(2,0),所以DA=1,PD=|y|,PA2=PD2+DA2=y2+1,分三种情况讨论解答:当PA=AB即PA2=AB2=10时;当PB=AB即PB2=AB2=10时;当PA=PB即PA2=PB2时.
解:(1)由y=﹣3x+3得,当x=0时,y=3;当y=0时,x=1
∴A(1,0)、B(0,3).
(2)把点A(1,0)、B(0,3)代入y=a(x﹣2)2+k得:
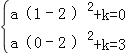
解得![]()
∴抛物线的函数表达式为y=(x﹣2)2﹣1.
(3)∵AO=1,BO=3,
∴AB=![]() .
.
设对称x轴交于点D,P(2,y),D(2,0),
∴DA=1,PD=|y|,PA2=PD2+DA2=y2+1,
当PA=AB即PA2=AB2=10时,
∴y2+1=10,
解得y=±3
∴P(2,±3),
但当P(2,﹣3)时,P、A、B在同一条直线上,不合题意舍去.
∴P1(2,3),
当PB=AB即PB2=AB2=10时,如图,过B作BE⊥对称轴于点E,
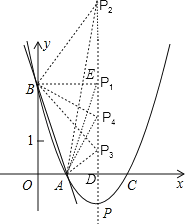
则E(2,3),EB=2,PE2=(y﹣3)2,
∴PB2=PE2+BE2=(y﹣3)2+4=10,
解得![]()
∴P2(2,3+![]() )、P3(2,3﹣
)、P3(2,3﹣![]() ),当PA=PB即PA2=PB2时,
),当PA=PB即PA2=PB2时,
y2+1=(y﹣3)2+4
解得y=2,
∴P4(2,2).
综上所述,所求的点为P1(2,3),P2(2,3+![]() ),P3(2,3﹣
),P3(2,3﹣![]() ),P4(2,2).
),P4(2,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=x2﹣1与x轴交点的个数( )
A.3
B.2
C.1
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.四边相等的四边形是菱形
B.一组对边相等,另一组对边平行的四边形是菱形
C.对角线互相垂直的四边形是菱形
D.对角线互相平分的四边形是菱形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某市7月1日至10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择7月1日至7月8日中的某一天到达该市,并连续停留3天,则此人在该市停留期间有且仅有1天空气质量优良的概率是( )

A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面,如图,A、B、C、D、E、F所持的纸牌的前面分别写有六个算式:66;63+63;(63)3;(2×62)×(3×63);(22×32)3;(64)3÷62.游戏规定:所持算式的值相等的两个人是朋友.如果现在由同学A来找他的朋友,他可以找谁呢?说说你的看法.
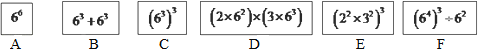
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P1 (a -1,1)和P2 (2,b +1)关于 y轴对称,求 a,b的值.
相关试题

