【题目】如图,已知OA,OB是☉O的半径,C为![]() 的中点,M,N分别是OA,OB的中点,求证:MC=NC.
的中点,M,N分别是OA,OB的中点,求证:MC=NC.

参考答案:
【答案】证明见解析
【解析】试题分析: 连接OC,根据C是![]() 的中点,易得到
的中点,易得到![]() ,由同圆中等弧对的圆心角相等可得∠AOC=∠BOC;由OA=OB,M,N分别为OA,OB的中点可得OM=ON,由边角边定理可以判断△MOC≌△NOC,从而可得到MC=NC.
,由同圆中等弧对的圆心角相等可得∠AOC=∠BOC;由OA=OB,M,N分别为OA,OB的中点可得OM=ON,由边角边定理可以判断△MOC≌△NOC,从而可得到MC=NC.
证明:连接OC.
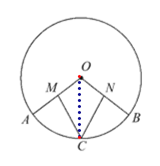
∵C为![]() 的中点,∴
的中点,∴![]() =
=![]() ,
,
∴∠MOC=∠NOC.
又∵M,N分别是OA,OB的中点,
∴OM=![]() OA,ON=
OA,ON=![]() OB,
OB,
∴OM=ON.
又∵OC=OC,
∴△OMC≌△ONC,∴MC=NC.
点睛:本题考查三角形全等的判定方法,弧与圆心角之间的关系,解题的关键是灵活运用三角形全等的判定方法及在等圆或同圆中相等的弧所对的圆心角相等这些定理;
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)a5a3a=__(2)(a5)3÷a6=__(3)(﹣2x2y)3=___
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式成立的是( )
A.x2+x2=x4B.2a2﹣a2=2C.(2a)2=2a2D.2a2a2=2a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2x2)3的结果是( )
A. ﹣6x5B. 6x5C. 8x6D. ﹣8x6
-
科目: 来源: 题型:
查看答案和解析>>【题目】用代数式表示“m加上n的和的立方”_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的面积是60,请完成下列问题:
(1)如图1,若AD是△ABC的BC边上的中线,则△ABD的面积________△ACD的面积(填“>”“<”或“=”)
(2)如图2,若CD、BE分别是△ABC的AB、AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO , 同理:S△CEO=S△AEO , 设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y由题意得:S△ABE=
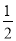 S△ABC=30,S△ADC=
S△ABC=30,S△ADC=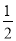 S△ABC=30,可列方程组为:
S△ABC=30,可列方程组为:  , 解得
, 解得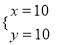 ,通过解这个方程组可得四边形ADOE的面积为________ .
,通过解这个方程组可得四边形ADOE的面积为________ . 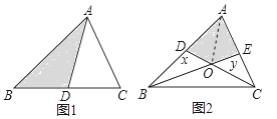
-
科目: 来源: 题型:
查看答案和解析>>【题目】当a=﹣2时,求a2(2a+1)=_____.
相关试题

