搜索
【题目】已知方程x2+100x+10=0的两根分别为x1 ， x2 ， 则x1x2﹣x1﹣x2的值等于 ．
参考答案：
【答案】110
【解析】解：∵方程x2+100x+10=0的两根分别为x1 ， x2 ， ∴x1+x2=﹣100，x1x2=10，
∴x1x2﹣x1﹣x2=x1x2﹣（x1+x2）=10﹣（﹣100）=110．
所以答案是：110．
【考点精析】通过灵活运用根与系数的关系，掌握一元二次方程ax2+bx+c=0（a≠0）的根由方程的系数a、b、c而定；两根之和等于方程的一次项系数除以二次项系数所得的商的相反数；两根之积等于常数项除以二次项系数所得的商即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】实数8的立方根是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【问题一】：观察下列等式
， 
， 
，将以上三个等式两边分别相加得：
．（1）猜想并写出：
_____________． （2）直接写出下列各式的计算结果：
①
____________； ②
______________． （3）探究并计算：
①
． ②
【问题二】：为了求
的值，可令
，则
，因此
，所以．
.仿照上面推理计算：
（1）求
的值；（2）求
的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】现实生活中，如果收入1000元记作+1000元，那么﹣800表示（ ）
A. 支出800元 B. 收入800元 C. 支出200元 D. 收入200元
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察图1：每个小正方形的边长均是1，我们可以得到小正方形的面积为1。
（1）图1中阴影正方形的面积是______，并由面积求正方形的边长，可得边长AB长为________；
（2）在图2：3×3正方形方格中，由题（1）的解题思路和方法，设计一个方案画出长为
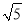的线段，并说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1，已知锐角△ABC中，分别以AB、AC为边向△ABC外作等边△ABD和等边△ACE，连结BE、CD，则线段BE与线段CD的数量关系是______．
（2）如图2，已知锐角△ABC中，分别以AB、AC为边向△ABC外作等腰直角△ABD和等腰直角△ACE，连结BE、CD，猜想线段BE与线段CD的有什么位置关系？并证明你的猜想．
（3）如图3，已知锐角△ABC中，分别以AB、AC为边向△ABC外作正方形ABDE和正方形ACFG，连接CE、BG，请写出线段CE与线段BG有什么关系？不需证明．
图1 图2 图3
-
科目： 来源： 题型：
查看答案和解析>>【题目】（6分）小聪是个数学爱好者，他发现从1开始，连续几个奇数相加，和的变化规律如右表所示：
加数个数
连续奇数的和S
1
1=
2
1+3=22
3
1+3+5=32
4
1+3+5+7=42
5
1+3+5+7+9=52
n
…
（1）如果n=7，则S的值为 ；
（2）求1+3+5+7+…+199的值；
（3）求13+15+17+…+79的值．
相关试题
