【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元时,则每个月少买5件(每件售价不能高于65元),设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每个月的利润恰为3200元?根据以上结论,请你直接写出售价在什么范围内,每个月的利润不低于3200元?
参考答案:
【答案】(1)y=﹣5x2+160x+2100(0<x≤15且x为整数);(2)当售价定为每件65元,每个月的利润最大,最大的月利润是3375元.(3)售价在不低于60且不高于65元之间时,每个月的利润不低于3200元.
【解析】
试题分析:(1)先求得销售量与上涨价格的关系式,然后再根据销售利润=件数×每件的利润列出关系式;
(2)先求得抛物线的对称轴,然后依据二次函数的性质确定出最大利润和此时的售价;
(3)令y=3200,得到关于x的一元二次方程,然后解得x的值即可,然后根据二次函数的性质可求得自变量的范围.
解:(1)由题意得:y=(210﹣5x)(50+x﹣40)
=﹣5x2+160x+2100(0<x≤15且x为整数);
(2)∵x=﹣![]() =﹣
=﹣![]() =16,
=16,
∴抛物线的对称轴为x=16,
∵a=﹣5<0,
∴当0<x≤15时,y随x的增大而增大.
∴当x=15时,每个月的获利最大,最大值为3375元.
50+15=65元.
∴当售价定为每件65元,每个月的利润最大,最大的月利润是3375元.
(3)当y=3200时,﹣5x2+160x+2100=3200,
解得:x1=10,x2=22(舍去).
∴当x=10时,即定价=50+10=60元.
∴当售价定为每件60元时,每个月的利润为3200元.
当售价在不低于60且不高于65元之间时,每个月的利润不低于3200元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. “打开电视机,它正在播广告”是必然事件
B. “一个不透明的袋中装有8个红球,从中摸出一个球是红球”是随机事件
C. 为了了解我市今年夏季家电市场中空调的质量,不宜采用普查的调查方式进行
D. 销售某种品牌的凉鞋,销售商最感兴趣的是该品牌凉鞋的尺码的平均数
-
科目: 来源: 题型:
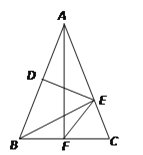
查看答案和解析>>【题目】如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则∠EFC=____°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列每组数分别是三根木棒的长度,能用它们摆成三角形的是( )
A. 3cm,4cm,8cm B. 8cm,7cm,15cm
C. 5cm,5cm,11cm D. 13cm,12cm,20cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
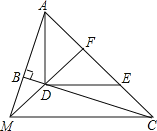
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分且相等的四边形是正方形
D.一组对边相等,另一组对边平行的四边形是平行四边形
相关试题

