【题目】如图,直线直线![]() 与双曲线
与双曲线![]() 交于A、B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(﹣3,﹣2).
交于A、B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(﹣3,﹣2).
(1)求直线和双曲线的解析式;
(2)求点C的坐标,并结合图象直接写出![]() 时x的取值范围.
时x的取值范围.

参考答案:
【答案】(1)![]() ,
,![]() ;(2)x<﹣2.
;(2)x<﹣2.
【解析】
试题分析:(1)由点B的坐标求出k=6,得出双曲线的解析式.求出A的坐标为(1,6),由点A和B的坐标以及待定系数法即可求出直线的解析式;
(2)求出点C的坐标为(﹣2,0),即可得出当y1<0时x的取值范围.
试题解析:(1)∵点B(﹣3,﹣2)在双曲线![]() 上,∴
上,∴![]() ,∴k=6,∴双曲线的解析式为
,∴k=6,∴双曲线的解析式为![]() .
.
把y=6代入![]() 得:x=1,∴A的坐标为(1,6),∵直线
得:x=1,∴A的坐标为(1,6),∵直线![]() 经过A、B两点,∴
经过A、B两点,∴![]() ,解得:
,解得:![]() ,∴直线的解析式为直线
,∴直线的解析式为直线![]() ;
;
(2)由直线![]() 得,x=﹣2,∴点C的坐标为(﹣2,0),当
得,x=﹣2,∴点C的坐标为(﹣2,0),当![]() 时x的取值范围是x<﹣2.
时x的取值范围是x<﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于
 PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为 .
PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店将巧克力包装成方形、圆形礼盒出售,且每盒方形礼盒的价钱相同,每盒圆形礼盒的价钱相同.小明原先想购买3盒方形礼盒和7盒圆形礼盒,但他身上的钱还少240元,如果改成购买7盒方形礼盒和3盒圆形礼盒,他身上的钱会剩下240元.每盒圆形礼盒比每盒方形礼盒多( )
A.90元B.140元C.100元D.120元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的对角线长为8cm,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于cm.

-
科目: 来源: 题型:
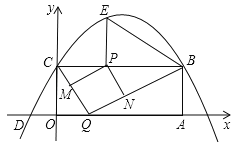
查看答案和解析>>【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线
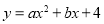 过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的标价为150元,若以8折降价出售.相对于进价仍获利20%,则该商品的进价为( )
A.120元
B.110元
C.100元
D.90元 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
(1)求证:EF是⊙O的切线;
(2)若DE=1,BC=2,求劣弧
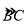 的长l.
的长l.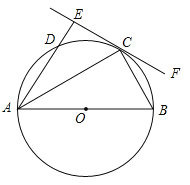
相关试题

