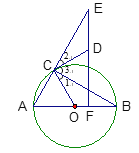
【题目】如图,AB为⊙O的直径,∠ABC=30°,ED⊥AB于点F,CD切⊙O于点C,交EF于点D.
(1)∠E= °;
(2)△DCE是什么特殊三角形?请说明理由;
(3)当⊙O的半径为1,BF=![]() 时,求证△DCE≌△OCB.
时,求证△DCE≌△OCB.

参考答案:
【答案】(1)30°; (2)△DCE为等腰三角形; 理由见解析;(3)证明见解析
【解析】【试题分析】(1)AB为⊙O的直径,则
![]() ,因为∠ABC=30°,则
,因为∠ABC=30°,则![]() ,因为ED⊥AB,则∠E=30°
,因为ED⊥AB,则∠E=30°
(2)△DCE为等腰三角形.理由:∠1=30°,根据同角的余角相等,得∠2=30°=∠E
得△DCE为等腰三角形.
(3)由(2)得△DCE∽△OCB,在Rt△ABC中, 求得BC=![]() =
=![]() . AF=AB-BF=2-
. AF=AB-BF=2-![]() =
=![]() ,在Rt△AEF中,
,在Rt△AEF中,
则AE=2AF=1+![]() ,CE=AE-AC=1+
,CE=AE-AC=1+![]() -1=
-1=![]() .
.
CE=BC=![]() ,△DCE≌△OCB得证。
,△DCE≌△OCB得证。
【试题解析】
(1)AB为⊙O的直径,则
![]() ,因为∠ABC=30°,则
,因为∠ABC=30°,则![]() ,因为ED⊥AB,则∠E=30°
,因为ED⊥AB,则∠E=30°
(2)△DCE为等腰三角形.
∵CD是⊙O的切线,∴∠OCD=90°.
即∠1+∠3=90°(如图).
∵AB为⊙O的直径,∴∠ACB=90°,
∴∠ECB=90°,即∠2+∠3=90°,
∴∠1=∠2.∵∠B=30°,∴∠A=60°;
∵OC=OB,∴∠1=∠B=30°,∴∠2=30°.
∵ED⊥AB于点F,∴∠E=90°-∠A=30°,
∴∠E=∠2,故△DCE的等腰三角形;
(3)证明:在Rt△ABC中,∵∠B=30°,
∴AC=![]() AB=
AB=![]() ×2=1.
×2=1.
∴BC=![]() =
=![]() .
.
AF=AB-BF=2-![]() =
=![]()
在Rt△AEF中,∵∠E=30°,
∴AE=2AF=1+![]() ,
,
∴CE=AE-AC=1+![]() -1=
-1=![]() .在△DCE和△OCB中,
.在△DCE和△OCB中,
∵∠E=∠2=∠B=∠1=30°,CE=BC=![]() ,∴△DCE≌△OCB.
,∴△DCE≌△OCB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(x,3)与点N(-2,y)关于x轴对称,则3x+2y= 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A.a2+a2=2a4
B.5m2﹣3m2=2
C.﹣x2y+yx2=0
D.4m2n﹣n2m=3m2n -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的底角是顶角的 2 倍,求这个三角形各个内角的度数.
-
科目: 来源: 题型:
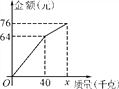
查看答案和解析>>【题目】小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了一部分西瓜后,余下的每千克降价0.4元,全部售完,销售金额与所卖西瓜数量之间的关系如图,求小李一共赚了多少元钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算8x8÷(-2x2)的结果是( )
A. -4x2B. -4x4
C. -4x6D. 4x6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果A2-B2=8,且A+B=4,那么A-B的值是____.
相关试题

