Question

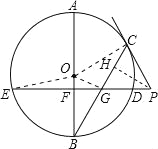
【题目】如图，已知AB是⊙O的直径，弦ED⊥AB于点F，点C是劣弧AD上的动点（不与点A、D重合），连接BC交ED于点G．过点C作⊙O的切线与ED的延长线交于点P．

（1）求证：PC=PG；

（2）当点G是BC的中点时，求证：；

（3）已知⊙O的半径为5，在满足（2）的条件时，点O到BC的距离为，求此时△CGP的面积．

Answer 1

【答案】(1)证明详见解析；(2)证明详见解析；(3)10.

【解析】

试题分析：（1）连结OC，根据切线的性质得OC⊥PC，根据余角的性质得到∠B=∠OCG，等量代换得到∠PCG=∠BGF，根据对顶角相等得∠BGF=∠PGC，于是得到∠PGC=∠PCG，根据等腰三角形的判定定理即可得到结论；

（2）连结OG，由点G是BC的中点，根据垂径定理的推论得OG⊥BC，BG=CG，根据相似三角形的性质得到，等量代换得到结论；

（3）连结OE，OG=OG=，在Rt△OBG中，利用勾股定理计算出BG=，再利用可计算出BF，从而得到OF=1，根据三角形的面积公式即可得到结论．

试题解析：（1）连结OC，如图，

∵PC为⊙O的切线，

∴OC⊥PC，

∴∠OCG+∠PCG=90°，

∵ED⊥AB，

∴∠B+∠BGF=90°，

∵OB=OC，

∴∠B=∠OCG，

∴∠PCG=∠BGF，

而∠BGF=∠PGC，

∴∠PGC=∠PCG，

∴PC=PG；

（2）解：CG、BF、BO三者之间的数量关系为．理由如下：

连结OG，如图，

∵点G是BC的中点，

∴OG⊥BC，BG=CG，

∴∠OGB=90°，

∵∠OBG=∠GBF，

∴Rt△BOG∽Rt△BGF，

∴BG：BF=BO：BG，

∴，

∴；

（3）解：连结OE，如图，

由（2）得OG⊥BC，

∴OG=，

在Rt△OBG中，OB=5，

∴BG==，

由（2）得BG2=BOBF，

∴BF==4，

∴OF=1，

∴FG==2，

过P作PH⊥BC于H，

∵PC=PG，

∴GH=CG=BG=，

∵∠PHG=∠BFG=90°，∠BGF=∠DGH，

∴△BFG∽△PHG，

∴，即，

∴PH=，

∴△CGP=CGPH=××=10．