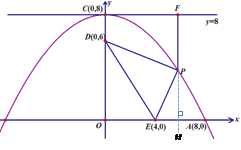
【题目】如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.
(1)求抛物线的解析式;
(2)猜想并探究:对于任意一点P,PD与PF的差是否为固定值?如果是,请求出此定值;如果不是,请说明理由;
(3)求:①当△PDE的周长最小时的点P坐标;②使△PDE的面积为整数的点P的个数.

参考答案:
【答案】(1)抛物线的解析式为y=﹣![]() x2+8;(2)PD与PF的差是定值,PD﹣PF=2;(3)①P(4,6),此时△PDE的周长最小;②共有11个令S△DPE为整数的点.
x2+8;(2)PD与PF的差是定值,PD﹣PF=2;(3)①P(4,6),此时△PDE的周长最小;②共有11个令S△DPE为整数的点.
【解析】(1)设抛物线的解析式为y=a(x+h)2+k
∵点C(0,8)是它的顶点坐标, ∴y=ax2+8
又∵经过点A(8,0),
有64a+8=0,解得a=![]()
故抛物线的解析式为:y=![]() x2+8;
x2+8;
(2)是定值,解答如下:
设P(a,![]() a2+8),则F(a,8),
a2+8),则F(a,8),
∵D(0,6),
∴PD=![]()
PF=![]() ,
,
∴PD﹣PF=2;
(3)当点P运动时,DE大小不变,则PE与PD的和最小时,△PDE的周长最小,
∵PD﹣PF=2,∴PD=PF+2,
 ∴PE+PD=PE+PF+2,
∴PE+PD=PE+PF+2,
∴当P、E、F三点共线时,PE+PF最小,
此时点P,E的横坐标都为4,
将x=4代入y=![]() x2+8,得y=6,
x2+8,得y=6,
∴P(4,6),此时△PDE的周长最小.
过点P做PH⊥x轴,垂足为H.
设P(a,![]() a2+8)
a2+8)
∴PH=![]() a2+8,EH=a-4,OH=a
a2+8,EH=a-4,OH=a
S△DPE=S梯形PHOD-S△PHE-S△DOE
=![]()
=![]()
=![]()
∵点P是抛物线上点A,C间的一个动点(含端点)
∴0≤a≤8
当a=6时,S△DPE取最大值为13.
当a=0时,S△DPE取最小值为4.
即4≤S△DPE≤13
其中,当S△DPE=12时,有两个点P.
所以,共有11个令S△DPE为整数的点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各对量中,不具有相反意义的是( )
A.胜3局与负3局
B.收入3000元与增加3000元
C.气温升高4℃与气温降低10℃
D.转盘逆时针转3圈与顺时针转5圈 -
科目: 来源: 题型:
查看答案和解析>>【题目】中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图1、图2补充完整;
(3)现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).

-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P在X轴的上方,Y轴的左侧,且到X轴的距离为3,到Y轴的距离为4,则点P的坐标是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,二次函数y=ax2+bx+c的图象中,王刚同学观察得出了下面四条信息:(1)b2﹣4ac>0;(2)c>1;(3)2a﹣b<0;(4)a+b+c<0,其中错误的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正数的平方根是3a+4和5-6a,则这个正数是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
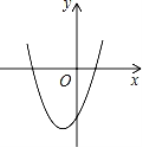
A. y1<y2B.y1>y2C.y的最小值是﹣3 D.y的最小值是﹣4
相关试题

