【题目】设函数f(x)= ![]() ﹣2+2alnx.
﹣2+2alnx.
(1)讨论函数f(x)的单调性;
(2)若f(x)在区间[ ![]() ,2]上的最小值为0,求实数a的值.
,2]上的最小值为0,求实数a的值.
参考答案:
【答案】
(1)解:f′(x)=﹣ ![]() +
+ ![]() =
= ![]() (x>0).
(x>0).
a≤0时,f′(x)<0,此时函数f(x)在(0,+∞)上单调递减.
a>0时,f′(x)= ![]() ,则x∈
,则x∈ ![]() 时,函数f(x)单调递减;
时,函数f(x)单调递减;
x∈ ![]() 时,函数f(x)单调递增
时,函数f(x)单调递增
(2)解:由(1)可得:
①a≤0时,函数f(x)在[ ![]() ,2]上单调递减,则f(2)=1﹣2+2aln2=0,解得a=
,2]上单调递减,则f(2)=1﹣2+2aln2=0,解得a= ![]() ,舍去.
,舍去.
②a>0时,
(i) ![]() ≥2,即0<a≤
≥2,即0<a≤ ![]() 时,f(x)在[
时,f(x)在[ ![]() ,2]上单调递减,则f(2)=1﹣2+2aln2=0,解得a=
,2]上单调递减,则f(2)=1﹣2+2aln2=0,解得a= ![]() ,舍去.
,舍去.
(ii)0< ![]() ,即a≥2时,f(x)在[
,即a≥2时,f(x)在[ ![]() ,2]上单调递增,则f(
,2]上单调递增,则f( ![]() )=4﹣2+2aln
)=4﹣2+2aln ![]() =0,解得a=
=0,解得a= ![]() <2,舍去.
<2,舍去.
(iii) ![]() ,即
,即 ![]() 时,f(x)在[
时,f(x)在[ ![]() ,
, ![]() )上单调递减,在
)上单调递减,在 ![]() 上单调递增.
上单调递增.
则f( ![]() )=2a﹣2+2aln
)=2a﹣2+2aln ![]() =0,化为:2a﹣2=2alna,
=0,化为:2a﹣2=2alna,
令g(x)=2x﹣2﹣2xlnx(x>0),g(1)=0,
g′(x)=2﹣2lnx﹣2=﹣2lnx,可得x>1时,函数g(x)单调递减,1>x>0时,函数g(x)单调递增.
∴x=1时,函数g(x)取得极大值即最大值.
∴g(x)≤g(1)=0,因此2a﹣2=2alna有唯一解a=1.满足条件.
综上可得:a=1.
【解析】(1)f′(x)=﹣ ![]() +
+ ![]() =
= ![]() (x>0).分类讨论:a≤0时,a>0时,即可得出单调性.(2)由(1)可得:①a≤0时,函数f(x)在[
(x>0).分类讨论:a≤0时,a>0时,即可得出单调性.(2)由(1)可得:①a≤0时,函数f(x)在[ ![]() ,2]上单调递减,可得f(2)=0,解得a.②a>0时,分类讨论:(i)
,2]上单调递减,可得f(2)=0,解得a.②a>0时,分类讨论:(i) ![]() ≥2,即0<a≤
≥2,即0<a≤ ![]() 时;(ii)0<
时;(ii)0< ![]() ,即a≥2时;(iii)
,即a≥2时;(iii) ![]() ,即
,即 ![]() 时,利用其单调性即可得出极值与最值.
时,利用其单调性即可得出极值与最值.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥ABC﹣A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2
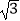 .
. 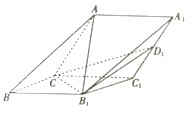
(1)求证:AB1⊥CC1;
(2)若AB1=3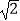 ,D1为线段A1C1上的点,且三棱锥C﹣B1C1D1的体积为
,D1为线段A1C1上的点,且三棱锥C﹣B1C1D1的体积为 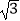 ,求
,求 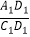 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年二十国集团领导人峰会(简称“G20峰会”)于9月4日至5日在浙江杭州召开,为保证会议期间交通畅通,杭州市已发布9月1日至7日为“G20峰会”调休期间.据报道对于杭州市民:浙江省旅游局联合11个市开展一系列旅游惠民活动,活动内容为:“本省游”、“黄山游”、“黔东南游”,某旅游公司为了解群众出游情况,拟采用分层抽样的方法从有意愿“本省游”、“黄山游”、“黔东南游”这三个区域旅游的群众中抽取7人进行某项调查,已知有意愿参加“本省游”、“黄山游”、“黔东南游”的群众分别有360,540,360人.
(1)求从“本省游”、“黄山游”、“黔东南游”,三个区域旅游的群众分别抽取的人数;
(2)若从抽得的7人中随机抽取2人进行调查,用列举法计算这2人中至少有1人有意愿参加“本省游”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点A(0,1)的椭圆C:
 +
+  =1(a>b>0)的左右焦点分别为F1、F2 , B为椭圆上的任意一点,且
=1(a>b>0)的左右焦点分别为F1、F2 , B为椭圆上的任意一点,且  |BF1|,|F1F2|,
|BF1|,|F1F2|,  |BF2|成等差数列.
|BF2|成等差数列.
(1)求椭圆C的标准方程;
(2)直线l:y=k(x+2)交椭圆于P,Q两点,若点A始终在以PQ为直径的圆外,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,直线l的参数方程为
 ,以原点为极点,x轴正半轴为极轴建立极坐标系,圆C 的极坐标方程为
,以原点为极点,x轴正半轴为极轴建立极坐标系,圆C 的极坐标方程为  .
.
(1)写出直线l的普通方程及圆C 的直角坐标方程;
(2)点P是直线l上的,求点P 的坐标,使P 到圆心C 的距离最小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|2x﹣a|+a.
(1)当a=3时,求不等式f(x)≤6的解集;
(2)设函数g(x)=|2x﹣3|,x∈R,f(x)+g(x)≥5,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合
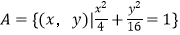 ,B={(x,y)|y=3x},则A∩B的子集的个数是( )
,B={(x,y)|y=3x},则A∩B的子集的个数是( )
A.4
B.3
C.2
D.1
相关试题

