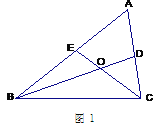
【题目】(1)如图1,在△ABC中∠A=60 ,BD、CE均为△ABC的角平分线且相交于点O.
①填空:∠BOC= 度;
②求证:BC=BE+CD.(写出求证过程)
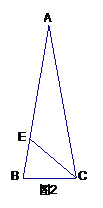
(2)如图2,在△ABC中,AB=AC=m,BC=n, CE平分∠ACB.
①若△ABC的面积为S,在线段CE上找一点M,在线段AC上找一点N,使得AM+MN的值最小,则AM+MN的最小值是 .(直接写出答案);
②若∠A=20°,则△BCE的周长等于 .(直接写出答案).
参考答案:
【答案】(1)①120;②证明见解析;(2)①![]() (或
(或![]() );②m
);②m
【解析】试题分析:(1)①根据三角形内角和定理得到∠BOC=180°-∠OBC-∠OCB,则2∠BOC=360°-2∠OBC-2∠OCB,再根据角平分线的定义得∠ABC=2∠OBC,∠ACB=2∠OCB,则2∠BOC=360°-∠ABC-∠ACB,易得∠BOC=90°+![]() ∠A,由∠A=60 即可得∠BOC的值;
∠A,由∠A=60 即可得∠BOC的值;
②采用截长法在在BC上截取BF=BE,连接OF,由边角边证得△EBO≌△FBO,再由角边角证得△DCO≌△FCO,即可得证;
(2)①当AM⊥BC时,AM+MN的值最小;
②在CA上截取CD=CB,以E为圆心EC为半径画弧,与AC交于点F,通过构造全等三角形,利用等腰三角形的判定和性质即可求解.
试题解析:(1)①在△OBC中,∠BOC=180°-∠OBC-∠OCB,
∴2∠BOC=360°-2∠OBC-2∠OCB,
∵BD、CE均为△ABC的角平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴2∠BOC=360°-∠ABC-∠ACB,
∴∠BOC=90°+![]() ∠A,
∠A,
∵∠A=60 ,
∴∠BOC=90°+![]() ×60 =120°;
×60 =120°;
故答案为:120°;
②证明:由(1)①∠BOC=120°,
∴∠BOE=∠COD=180°-120°=60°,
在BC上截取BF=BE,连接OF,

∵BD平分∠ABC,
∴∠EBO=∠FBO,
又∵BO=BO(公共边相等)
∴△EBO≌△FBO(SAS)
∴∠BOF=∠BOE=60°,
∴∠COF=∠BOC-∠BOF=120°-60°=60°=∠COD,
∵CE平分∠ACB,
∴∠DCO=∠FCO,
又∵CO=CO(公共边相等)
∴△DCO≌△FCO(ASA)
∴CD=CF,
∴BC=BF+CF=BE+CD;
(2)①如图:

当AM⊥BC时,与BC交于点D,过M作MN⊥AC交AC与点D,
∵CE平分∠ACB,
∴DM=DN,
∴AD=AM+MD=AM+MN,
此时,AM+MN的值最小,
由S△ABC=![]() BC·AD,BC=n,△ABC的面积为S,
BC·AD,BC=n,△ABC的面积为S,
得AD=![]() ,
,
或∵AB=AC, AD⊥BC, AB=AC=m,BC=n,
∴BD=CD=![]() ,
,
在Rt△ACD中,由勾股定理得AD=![]() ;
;
故答案为: ![]() (或
(或![]() );
);
②如图:在CA上截取CD=CB,以E为圆心EC为半径画弧,与AC交于点F,

∵AB=AC=m,∠A=20°,
∴∠B=∠C=80°,
∵CE平分∠ACB,
∴∠BCE=∠DCE=40°,
∵CE=CE,
∴△BCE≌△DCE,
∴∠CDE=∠B=80°,∠DEC=∠BEC=60°,BE=DE,
∴∠CDE=40°,
∵EC=EF,
∴∠EFC=∠ECF=40°,
∴∠DEF=∠CDE-∠DFE=40°,
∴DE=DF,
∠AEF=∠DFE-∠A=40°-20°=20°,
∴EF=AF,
∴BE=DF,CE=AF,
∴△BCE的周长=BC+CE+BE=CD+AF+DF=AC=m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】共享单车近日成为市民新宠,越来越多的居民选择共享单车作为出行的交通工具,某中学课外兴趣小组为了了解某小区居民每周使用共享单车时间的情况,随机抽取了该小区部分使用共享单车的居民进行调查(问卷调查表如图所示),并用调查结果绘制了图①、图②两幅每周使用共享单车时间的人数统计图(均不完整),请根据统计图解答以下问题:
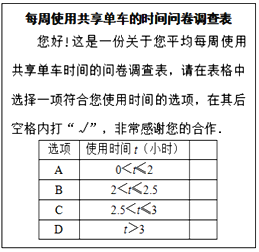
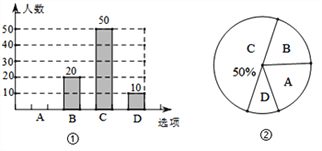
(1)本次接受问卷调查的共有 人;在扇形统计图中“D”选项所占的百分比为 ;
(2)扇形统计图中,“B”选项所对应扇形圆心角为 度;
(3)请补全条形统计图;
(4)若该小区共有1200名居民,请你估计该小区使用共享单车的时间在“A”选项的有多少人?
-
科目: 来源: 题型:
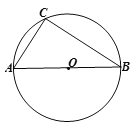
查看答案和解析>>【题目】已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.
(1)求⊙O的半径;
(2)请用尺规作图作出点P,使得点P在优弧CAB上时,△PBC的面积最大,请保留作图痕迹,并求出△PBC面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式x﹣5与2x﹣1的值相等,则x的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(x3)3=x9
B.(﹣2x)3=﹣6x3
C.2x2﹣x=x
D.x6÷x3=x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.
(1) 试说明DF=CE;
(2) 若AC=BF=DF,求∠ACE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积.

相关试题

