搜索
【题目】在平行四边形ABCD中，E，F分别为边AB，CD的中点，连接DE，BF，BD．
（1）求证：△ADE≌△CBF．
（2）若AD⊥BD，则四边形BFDE是什么特殊四边形？请证明你的结论．
参考答案：
【答案】（1）、证明过程见解析；（2）、菱形.
【解析】
试题分析：（1）、根据平行四边形的性质得到AD=BC，AB=CD，∠A=∠C，根据中点得到AE=CF，从而说明三角形全等；（2）、首先判断BFDE为平行四边形，根据直角三角形斜边上的中线的性质得到DE=BE，从而说明四边形BFDE为菱形.
试题解析：（1）、∵四边形ABCD为平行四边形 ∴AD=BC AB=CD ∠A=∠C
∵E，F分别为AB，CD的中点 ∴AE=CF ∴△ADE≌△CBF
、∵ABCD为平行四边形，E，F分别为AB，CD的中点 ∴DF=BE DF∥BE
∴四边形BFDE为平行四边形 ∵AD⊥BD ∴△ABD为直角三角形 DE为三角形斜边上的中线
∴DE=BE ∴四边形BFDE为菱形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】用科学记数法表示：0.000 45，正确的是( )
A. 4.5×104 B. 4.5×10－4 C. 4.5×10－5 D. 4.5×105
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平行四边形ABCD中，∠A=65°，则∠C的度数是______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图，且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根，有下列结论：①b2﹣4ac＞0；②abc＜0；③m＞2，其中正确结论的个数是（ ）
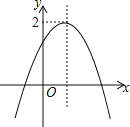
A．0 B．1 C．2 D．3
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=﹣x+3与x轴，y轴分别相交于点B、点C，经过B、C两点的抛物线y=ax2+bx+c与x轴的另一交点为A，点A在点B的左边，顶点为P，且线段AB的长为2．
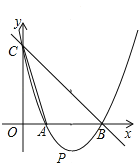
（1）求点A的坐标；
（2）求该抛物线的函数表达式；
（3）在抛物线的对称轴上是否存在点G，使|GC﹣GB|最大？若存在，求G点坐标；若不存在说明理由．
（4）连结AC，请问在x轴上是否存在点Q，使得以点P，B，Q为顶点的三角形与△ABC相似？若存在，请求出点Q的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点（-1，-5），且与正比例函数
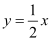的图象相交于点（2，a）．
（1）求a的值．
（2）求一次函数y=kx+b的表达式．
（3）在同一坐标系中，画出这两个函数的图象．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，
∠BAD＝45°，AD与BE交于点F，连接CF.
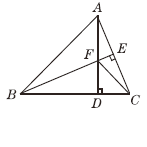
（1）求证：BF＝2AE；
（2）若CD＝
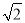，求AD的长.
相关试题
