搜索
【题目】有一副三角板
和
，其中
，
，
，
．
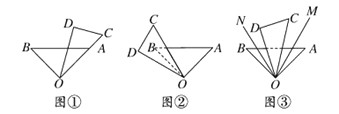
（1）如图①，点
，
，
在一条直线上，
的度数是______________．
（2）如图②，变化摆放位置将直角三角板绕点逆时针方向转动，若
恰好平分
，则
的度数是__________；
（3）如图③，当三角板摆放在
内部时，作射线
平分，射线
平分．如果三角板在内绕点任意转动，
的度数是否发生变化？如果不变，求其值；如果变化，说明理由．
参考答案：
【答案】（1）
；（2）
；（3）.
【解析】
（1）根据
计算即可；
（2）由角平分线的定义可求得
的度数，根据
计算即可；
（3）不发生变化，由角平分线的定义可求得
的度数，由
可求得其值.
解：（1）
，
的度数是；
（2）
平分
，
所以
的度数是；
（3）
的度数不发生变化.
，
平分， 
平分
所以的度数不发生变化，其值为.
-
科目： 来源： 题型：
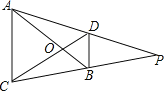
查看答案和解析>>【题目】如图，AB与CD相交于点O，且∠OAD=∠OCB，延长AD、CB交于点P，那么图中的相似三角形的对数为______ ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（10分）有甲、乙两个不透明的盒子，甲盒子中装有3张卡片，卡片上分别写着3
、7、9；乙盒子中装有4张卡片，卡片上分别写着2、4、6、8；盒子外有一张写着5的卡片．所有卡片的形状、大小都完全相同．现随机从甲、乙两个盒子中各取出一张卡片，与盒子外的卡片放在一起，用卡片上标明的数量分别作为一条线段的长度．（1）请用树状图或列表的方法求这三条线段能组成三角形的概率；
（2）求这三条线段能组成直角三角形的概率．
-
科目： 来源： 题型：
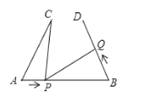
查看答案和解析>>【题目】如图,AB=6cm,AC=BD=4cm.∠CAB=∠DBA=60 ,点 P 在线段 AB 上以 1cm/s 的速度由点A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动。它们运动的时间为 t(s)，则点 Q的运动速度为________cm/s，使得 A. C. P 三点构成的三角形与 B. P、Q 三点构成的三角形全等。
-
科目： 来源： 题型：
查看答案和解析>>【题目】某一公路的道路维修工程，准备从甲、乙两个工程队选一个队单独完成．根据两队每天的工程费用和每天完成的工程量可知，若由两队合做此项维修工程，6天可以完成，共需工程费用385200元，若单独完成此项维修工程，甲队比乙队少用5天，每天的工程费用甲队比乙队多4000元，（1）若甲单独完成需要多少天？（2）从节省资金的角度考虑，应该选择哪个工程队？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
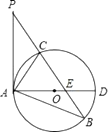
（1）求证：PA是⊙O的切线；
（2）过点C作CF⊥AD，垂足为点F，延长CF交AB于点G，若AGAB=12，求AC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】出租车司机小傅某天下午营运全是在东西走向的大道上行驶的．若如果规定向东为正，则行车里程（单位：km）如下：
＋11，－2，＋3，＋10，－11，＋5，－15，－8
（1）当把最后一名乘客送到目的地时，小傅距离出车地点的距离为多少？
（2）若每千米的营运额为7元，成本为1．5元/km，则这天下午他盈利多少元？
相关试题
