【题目】某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
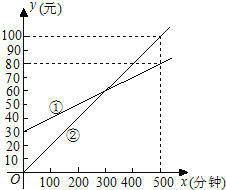
(1)有月租费的收费方式是 (填①或②),月租费是 元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
参考答案:
【答案】(1)①;30;(2)y1=0.1x+30; y2=0.2x;(3)见解析
【解析】
试题分析:(1)根据当通讯时间为零的时候的函数值可以得到哪种方式有月租,哪种方式没有,有多少;
(2)根据图象经过的点的坐标设出函数的解析式,用待定系数法求函数的解析式即可;
(3)求出当两种收费方式费用相同的时候自变量的值,以此值为界说明消费方式即可.
解:(1)①;30;
(2)设y1=k1x+30,y2=k2x,由题意得:将(500,80),(500,100)分别代入即可:
500k1+30=80,
∴k1=0.1,
500k2=100,
∴k2=0.2
故所求的解析式为y1=0.1x+30; y2=0.2x;
(3)当通讯时间相同时y1=y2,得0.2x=0.1x+30,解得x=300;
当x=300时,y=60.
故由图可知当通话时间在300分钟内,选择通话方式②实惠;
当通话时间超过300分钟时,选择通话方式①实惠;
当通话时间在300分钟时,选择通话方式①、②一样实惠.
-
科目: 来源: 题型:
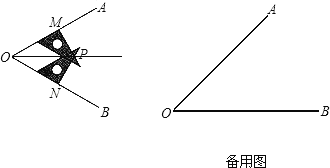
查看答案和解析>>【题目】小丽同学要画∠AOB的平分线,却没有量角器和圆规,于是她用三角尺按下面方法画角平分线:
①在∠AOB的两边上,分别取OM=ON;
②分别过点M、N作OA、OB的垂线,交点为P;
③画射线OP,则OP为∠AOB的平分线.
(1)请问:小丽的画法正确吗?试证明你的结论;
(2)如果你现在只有刻度尺,能否画一个角的角平分线?请你在备用图中试一试.(不需要写作法,但是要让读者看懂,你可以在图中标明数据)
-
科目: 来源: 题型:
查看答案和解析>>【题目】成都地铁自开通以来,发展速度不断加快,现已成为成都市民主要出行方式之一.今年4月29日成都地铁安全运输乘客约181万乘次,又一次刷新客流纪录,这也是今年以来第四次客流纪录的刷新,用科学记数法表示181万为( )
A.18.1×105 B.1.81×106 C.1.81×107 D.181×104
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣3,﹣1,1,3四个数中,比﹣2小的数是( )
A.﹣3 B.﹣1 C.1 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料并回答问题:
在解分式方程
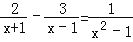 时,小明的解法如下:
时,小明的解法如下:解:方程两边同乘以(x+1)(x﹣1),得2(x﹣1)﹣3=1①
去括号,得2x﹣1=3﹣1 ②
解得x=

检验:当x=
 时,(x+1)(x﹣1)≠0 ③
时,(x+1)(x﹣1)≠0 ③所以x=
 是原分式方程的解 ④
是原分式方程的解 ④(1)你认为小明在哪里出现了错误 (只填序号)
(2)针对小明解分式方程出现的错误和解分式方程中的其他重要步骤,请你提出三条解分式方程时的注意事项;
(3)写出上述分式方程的正确解法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,请你作出猜想:当∠AMN= 时,结论AM=MN仍然成立.(直接写出答案,不需要证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点E,F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,∠EAF=90°,BC=12,EF=5.
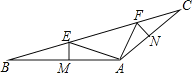
(1)求∠BAC的度数;
(2)求S△EAF.
相关试题

