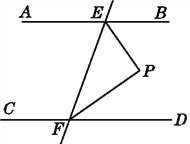
【题目】如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EP平分∠BEF,FP平分∠DFE.试说明:△PEF是直角三角形.
参考答案:
【答案】△PEF是直角三角形
【解析】试题分析:根据平行线的性质,由AB∥CD得到∠BEF+∠DFE =180°,再根据角平分线定义得∠PEF+∠PFE=![]() (∠BEF+∠DFE),然后计算出∠P=90°,根据直角三角形的定义即可得到△EPF是直角三角形.
(∠BEF+∠DFE),然后计算出∠P=90°,根据直角三角形的定义即可得到△EPF是直角三角形.
试题解析:
证明:因为AB∥CD,
所以∠BEF+∠DFE=180°.
又因为EP平分∠BEF,FP平分∠DFE,
所以∠PEF=![]() ∠BEF,∠PFE=
∠BEF,∠PFE=![]() ∠DFE.
∠DFE.
所以∠PEF+∠PFE=![]() (∠BEF+∠DFE)=90°.
(∠BEF+∠DFE)=90°.
又因为∠PEF+∠PFE+∠P=180°,
所以∠P=90°.
所以△PEF是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以直线上一点
 为端点作射线
为端点作射线 ,使
,使 .将一个直角三角板
.将一个直角三角板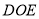 (其中
(其中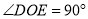 )的直角顶点放在点
)的直角顶点放在点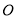 处.
处.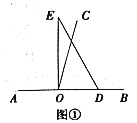
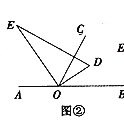
(1)如图①,若直角三角板
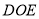 的一边
的一边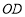 放在射线
放在射线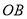 上,则
上,则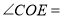 ____
____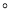 ;
;(2)如图②,将直角三角板
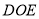 绕点
绕点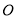 逆时针转动到某个位置,若
逆时针转动到某个位置,若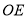 恰好平分
恰好平分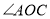 ,则
,则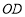 所在的射线是否为
所在的射线是否为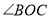 的平分线?请说明理由;
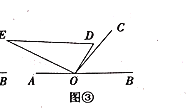
的平分线?请说明理由;(3)如图③,将含
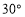 角的直角三角板
角的直角三角板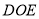 从图①的位置开始绕点
从图①的位置开始绕点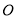 以每秒
以每秒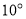 的速度逆时针旋转,设旋转角为
的速度逆时针旋转,设旋转角为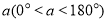 ,旋转的时间为
,旋转的时间为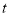 秒,在旋转过程中是否存在三角板的一条边与
秒,在旋转过程中是否存在三角板的一条边与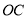 垂直?若存在,请直接写出此时
垂直?若存在,请直接写出此时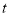 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
求1+2+22+23+24+……+22019的值.
解:设S=1+2+22+23+24+……+22019,
将等式两边同时乘以2,得
2S=2+22+23+24+…+22019+22020,
将下式减去上式得2S-S=22020-1,
请你仿照此法计算:
(1)1+2+22+23+24+…+210;
(2)1+3+32+33+34……+3n(其中n为正整数).
-
科目: 来源: 题型:
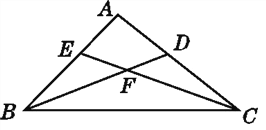
查看答案和解析>>【题目】如图,以CD为公共边的三角形是____________;∠EFB是____________的内角;在△BCE中,BE所对的角是____________,∠CBE所对的边是____________;以∠A为公共角的三角形是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个直角
 和
和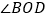 有公共顶点
有公共顶点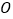 .下列结论:①
.下列结论:①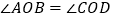 ;②
;②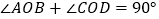 ;③若
;③若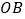 平分
平分 ,则
,则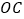 平分
平分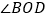 ;④
;④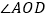 的平分线与
的平分线与 的平分线是同一条射线.其中结论正确的个数是( )
的平分线是同一条射线.其中结论正确的个数是( )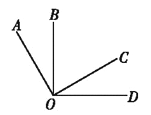
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
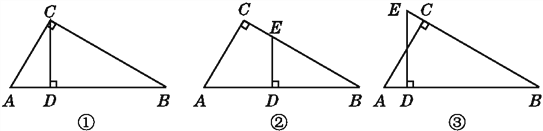
查看答案和解析>>【题目】(1)如图①,CD是直角三角形ABC斜边AB上的高,图中有与∠A相等的角吗?为什么?
(2)如图②,把图①中的CD平移到ED处,图中还有与∠A相等的角吗?为什么?
(3)如图③,把图①中的CD平移到ED处,交BC的延长线于点E,图中还有与∠A相等的角吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式,属于二元一次方程的个数有( )
①xy+2x﹣y=7;②4x+1=x﹣y;③
 +y=5;④x=y;⑤x2﹣y2=2;⑥6x﹣2y;⑦x+y+z=1;⑧y(y﹣1)=2x2﹣y2+xy
+y=5;④x=y;⑤x2﹣y2=2;⑥6x﹣2y;⑦x+y+z=1;⑧y(y﹣1)=2x2﹣y2+xyA.1B.2C.3D.4
相关试题

