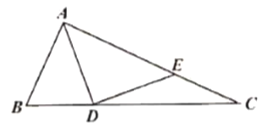
【题目】如图，是的角平分线，在上，，若，，，则________________．

【答案】

【解析】

过点D作DM⊥AC于点M，作DN⊥AB于点N，设CM=，表示出CD和DM，再证明Rt△AMD≌Rt△AND，根据AB+CE=7，列出等式解出x，过点B作AC的平行线交AD延长线于点F，证明△BFD∽△CAD，从而求出AE长.

过点D作DM⊥AC于点M，作DN⊥AB于点N，如图，

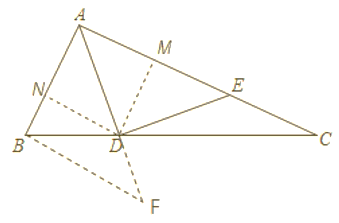
设CM=，

∵，

∴CD=7x,

∴，

∵AD平分∠BAC，

∴DN=DM=3x,

∵BD=3，

∴，

∵AD=DE，

∴，

在Rt△AMD和Rt△AND中，

∴Rt△AMD≌Rt△AND（HL），

∴AM=AN，

∴AN=EM，

∵AB+CE=7，

∴BN+AN+CE=7，

∴BN+EM+CE=7，

∴BN+CM=7，

∴BN=7-CM，

∴，

∴，

解得：，

∴CD=，，，

过点B作AC的平行线交AD延长线于点F，

则∠F=∠CAD，

∵AD平分∠BAC，

∴∠BAD=∠CAD，

∴∠BAD=∠F，

∴BF=AB，

∵BF∥AC，

∴△BFD∽△CAD，

∴，

∴，

∴，

设AN=AM=y，则AB=AN+BN=，

AC=AM+CM=，

∴，

解得：，

∴AE=2y，

故答案为：.

关闭