Question

【题目】如图，在△ABC中，AB=AC，DE是过点A的直线，BD⊥DE于D，CE⊥DE于点E．

（1）若B、C在DE的同侧（如图1所示）且AD=CE，AB与AC垂直吗？为什么？

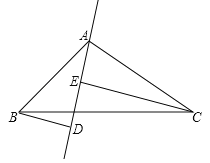
（2）若B、C在DE的两侧（如图2所示），其他条件不变，AB与AC是否垂直吗？若垂直请给出证明；若不垂直，请说明理由．

Answer 1

【答案】（1）证明见解析；（2）AB⊥AC．

【解析】试题分析：（1）由已知条件，证明△ABD≌△CAE，再利用角与角之间的关系求证∠BAD+∠CAE=90°，即可得到AB⊥AC；

（2）同（1），先证△ABD≌△CAE，再利用角与角之间的关系求证∠BAD+∠CAE=90°，即可证明AB⊥AC．

试题解析：（1）证明：∵BD⊥DE，CE⊥DE，∴∠ADB=∠AEC=90°，在Rt△ABD和Rt△ACE中，∵AB=AC，AD=CE，∴Rt△ABD≌Rt△CAE，∴∠DAB=∠ECA，∠DBA=∠ACE．

∵∠DAB+∠DBA=90°，∠EAC+∠ACE=90°，∴∠BAD+∠CAE=90°．

∠BAC=180°﹣（∠BAD+∠CAE）=90°，∴AB⊥AC．

（2）AB⊥AC．理由如下：

同（1）一样可证得△ABD≌△CAE，∴∠DAB=∠ECA，∠DBA=∠EAC，∵∠CAE+∠ECA=90°，∴∠CAE+∠BAD=90°，即∠BAC=90°，∴AB⊥AC．