Question

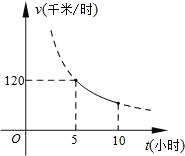
【题目】一辆客车从甲地出发前往乙地，平均速度v（千米/小时）与所用时间t（小时）的函数关系如图所示，其中60≤v≤120．

（1）直接写出v与t的函数关系式；

（2）若一辆货车同时从乙地出发前往甲地，客车比货车平均每小时多行驶20千米，3小时后两车相遇．

①求两车的平均速度；

②甲、乙两地间有两个加油站A、B，它们相距200千米，当客车进入B加油站时，货车恰好进入A加油站（两车加油的时间忽略不计），求甲地与B加油站的距离．

Answer 1

【答案】（1）v与t的函数关系式为v=（5≤t≤10）；（2）①客车和货车的平均速度分别为110千米/小时和90千米/小时；②甲地与B加油站的距离为220或440千米．

【解析】

试题分析：（1）利用时间t与速度v成反比例可以得到反比例函数的解析式；

（2）①由客车的平均速度为每小时v千米，得到货车的平均速度为每小时（v-20）千米，根据一辆客车从甲地出发前往乙地，一辆货车同时从乙地出发前往甲地，3小时后两车相遇列出方程，解方程即可；

②分两种情况进行讨论：当A加油站在甲地和B加油站之间时；当B加油站在甲地和A加油站之间时；都可以根据甲、乙两地间有两个加油站A、B，它们相距200千米列出方程，解方程即可．

试题解析：（1）设函数关系式为v=，

∵t=5，v=120，

∴k=120×5=600，

∴v与t的函数关系式为v=（5≤t≤10）；

（2）①依题意，得

3（v+v-20）=600，

解得v=110，

经检验，v=110符合题意．

当v=110时，v-20=90．

答：客车和货车的平均速度分别为110千米/小时和90千米/小时；

②当A加油站在甲地和B加油站之间时，

110t-（600-90t）=200，

解得t=4，此时110t=110×4=440；

当B加油站在甲地和A加油站之间时，

110t+200+90t=600，

解得t=2，此时110t=110×2=220．

答：甲地与B加油站的距离为220或440千米．