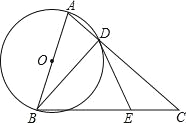
【题目】如图,在△ABC中,AC=BC,以AB为直径的⊙O交AC边于点D,点E在BC上,连结BD,DE,∠CDE=∠ABD.
(1)证明:DE是⊙O的切线;
(2)若BD=12,sin∠CDE=![]() ,求圆O的半径和AC的长.
,求圆O的半径和AC的长.
参考答案:
【答案】(1)详见解析;(2)圆O的半径为![]() ;AC=
;AC=![]() .
.
【解析】
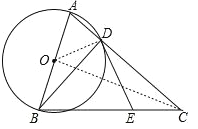
试题分析:(1)连结OD,如图,根据圆周角定理,由AB为⊙O的直径得∠ADO+∠ODB=90°,再由OB=OD得∠OBD=∠ODB,则∠ADO+∠ABD=90°,由于∠CDE=∠ABD,所以∠ADO+∠CDE=90°,然后根据平角的定义得∠ODE=90°,于是可根据切线的判定定理得到DE是⊙O的切线;(2)由于∠CDE=∠ABD,则sin∠CDE=sin∠ABD=![]() ,在Rt△ABD中,根据正弦的定义得sin∠ABD=
,在Rt△ABD中,根据正弦的定义得sin∠ABD=![]() =
=![]() ,设AD=5x,则AB=13x,由勾股定理得BD=12x,所以12x=12,解得x=1,得到AB=13,则圆O的半径为
,设AD=5x,则AB=13x,由勾股定理得BD=12x,所以12x=12,解得x=1,得到AB=13,则圆O的半径为![]() ;再连结OC,如图,由于CA=CB,OA=OB,根据等腰三角形的性质得CO⊥AB,则利用等角的余角相等可得到∠ACO=∠ABD,然后在Rt△ACO中,利用∠ACO的正弦可计算出AC的长.
;再连结OC,如图,由于CA=CB,OA=OB,根据等腰三角形的性质得CO⊥AB,则利用等角的余角相等可得到∠ACO=∠ABD,然后在Rt△ACO中,利用∠ACO的正弦可计算出AC的长.
试题解析:(1)证明:连结OD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,即∠ADO+∠ODB=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ADO+∠ABD=90°,
∵∠CDE=∠ABD,
∴∠ADO+∠CDE=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵∠CDE=∠ABD,
∴sin∠CDE=sin∠ABD=![]() ,
,
在Rt△ABD中,sin∠ABD=![]() =
=![]() ,
,
设AD=5x,则AB=13x,
∴BD=![]() =12x,
=12x,
∴12x=12,解得x=1,
∴AB=13,
∴圆O的半径为![]() ;
;
连结OC,如图,
∵CA=CB,OA=OB,
∴CO⊥AB,
∴∠ACO=∠ABD,
在Rt△ACO中,∵sin∠ACO=![]() =
=![]() ,
,
∴AC=![]() ×
×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式﹣x2+2x+3中的二次项系数是( )
A. ﹣1 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业今年1月份产值为a万元,2月份比1月份减少了15%,3月份比2月份增加了5%,则3月份的产值为( )
A.(a+15%)(a-5%)万元B.(a-15%)(a+5%)万元
C.a(1+15%)(1-5%)万元D.a(1-15%)(1+5%)万元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】第十三届全运会将于2017年8月在天津举行,其中足球项目承办场地为团泊足球场,该足球场占地163000平方米,将163000用科学记数法表示应为( )
A.163×103
B.16.3×104
C.1.63×105
D.0.163×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条公路的转弯处是一段圆弧(
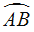 ).
).(1)用直尺和圆规作出
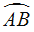 所在圆的圆心O;(要求保留作图痕迹,不写作法)
所在圆的圆心O;(要求保留作图痕迹,不写作法)(2)若
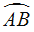 的中点C到弦AB的距离为20m,AB=80m,求
的中点C到弦AB的距离为20m,AB=80m,求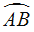 所在圆的半径.
所在圆的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE.

(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
相关试题

