【题目】如图,A,O,B在同一条直线上,∠AOD=∠BOD=∠EOC=90°,∠BOC∶∠AOE=3∶1.
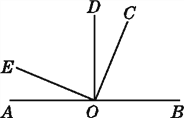
(1)求∠COD的度数.
(2)图中有哪几对角互为余角?
(3)图中有哪几对角互为补角?
参考答案:
【答案】答案见解析.
【解析】试题分析:(1)先求出∠BOC+∠AOE,再根据比值求出∠BOC,然后列式计算即可得解;
(2)根据互余的两个角的和等于90°找出即可;
(3)根据互补的两个角的和等于180°找出即可.
试题解析:(1)由A,O,B在同一条直线上得∠AOB=180°.
因为∠EOC=90°,所以∠AOE+∠BOC=180°-90°=90°.
又因为∠BOC∶∠AOE=3∶1,所以∠BOC=67.5°,
所以∠COD=∠BOD-∠BOC=90°-67.5°=22.5°.
(2)∠AOE与∠DOE,∠AOE与∠BOC,∠DOE与∠DOC,∠DOC与∠BOC互为余角.
(3)∠AOE与∠EOB,∠AOD与∠DOB,∠AOC与∠BOC,∠EOD与∠AOC,∠DOC与∠EOB,∠AOD与∠EOC,∠BOD与∠EOC互为补角.
-
科目: 来源: 题型:
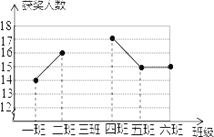
查看答案和解析>>【题目】某中学组织网络安全知识竞赛活动,其中七年级6个班组每班参赛人数相同,学校对该年级的获奖人数进行统计,得到每班平均获奖15人,并制作成如图所示不完整的折线统计图.
(1)请将折线统计图补充完整,并直接写出该年级获奖人数最多的班级是 班;
(2)若二班获奖人数占班级参赛人数的32%,则全年级参赛人数是 人;
(3)若该年级并列第一名有男、女同学各2名,从中随机选取2名参加市级比赛,请用列表或画树状图的方法求出恰好选中一男一女的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.3a+2a=5a2
B.a6÷a2=a3
C.(﹣3a3)2=9a6
D.(a+2)2=a2+4 -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ax+ay= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子有6个完全一样的球,分别写着数字1、2、3、4、5、6,从中摸出一个记下球上的数字,然后放进去,在摸一个球,则两次摸出球上的数字之和为5的概率为__________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系中,直线AB与x轴、y轴分别交于B、A两点,若OA、OB的长分别是方程若x-7mx+48=0的两根且OB>OA,AB=10.AC平分∠BAO交x轴于点C.
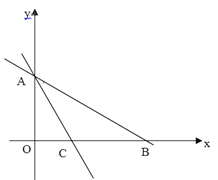
(1)求A、B两点的坐标.
(2)直线AC的解析式.
(3)直线AC上是否存在点P,使A、B、P三点构成的三角形为直角三角形?若存在,请直接写出P 点坐标;若不存在,请说明理由.
相关试题

