Question

【题目】 (1)如图1，纸片□ABCD中，AD=5,S□ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置，拼成四边形AEE′D,则四边形AEE′D的形状为（ ）

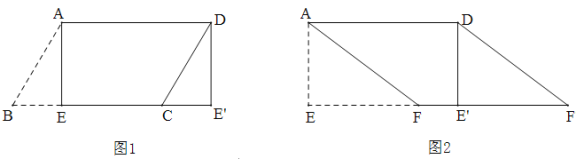
A.平行四边形 B.菱形 C.矩形 D.正方形

(2)如图2，在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4，剪下△AEF，将它平移至△DE′F′ 的位置，拼成四边形AFF′D

① 求证四边形AFF′D是菱形

② 求四边形AFF′D两条对角线的长.

Answer 1

【答案】（1）C；（2）①证明参见解析；② 3和.

【解析】

试题分析：（1）根据题意和有一个角是直角的平行四边形是矩形即可得出结论；（2）①计算出AF的长度，利用邻边相等的平行四边形是菱形即可得出结论；②连接AF′, DF,在Rt△AEF′中，利用勾股定理求出AF'，在Rt△DFE′中，利用勾股定理求出DF，于是可知四边形AFF′D两条对角线的长.

试题解析：(1)根据题意可知四边形ABCD是平行四边形，AE⊥BC,∠AEE'=90°，因为有一个角是直角的平行四边形是矩形，故C选项正确；(2) ①∵AF∥DF′且AF=DF′, ∴四边形AFF′D是平行四边形，因为S□ABCD=ADAE=15, AD=5 ,所以AE=3, 又因为EF=4 ,∠E=90°, 所以AF=5, 因为AD=5 , 所以AD=AF , 所以平行四边形AFF′D是菱形. ②如图， 连接AF′, DF,

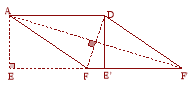
在Rt△AEF′中，AE=3, EF′=4+5=9, 所以AF′==3；在Rt△DFE′中，FE′=5-4=1, DE′=AE=3, 由勾股定理算出DF=，所以四边形AFF′D两条对角线的长分别是3和.