【题目】己知一次函数![]() ,
,
(1)无论 k为何值,函数图像必过定点,求该点的坐标;
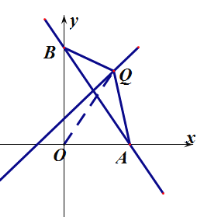
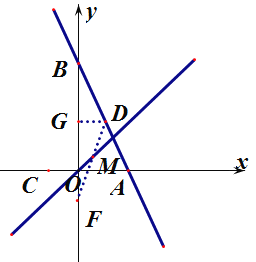
(2)如图 1,当 k=-![]() 时,该直线交 x 轴,y 轴于 A,B 两点,直线 l2:y=x+1 交 AB 于点 P,点 Q 是 l2 上一点,若 SABQ 6 ,求 Q 点的坐标;
时,该直线交 x 轴,y 轴于 A,B 两点,直线 l2:y=x+1 交 AB 于点 P,点 Q 是 l2 上一点,若 SABQ 6 ,求 Q 点的坐标;
(3)如图 2,在第 2 问的条件下,已知 D 点在该直线上,横坐标为 1,C 点在 x 轴负半轴, ABC=45 ,动点 M 的坐标为(a,a),求 CM+MD 的最小值.

参考答案:
【答案】(1)(![]() );(2)(3,4)或(-1,0);(3)
);(2)(3,4)或(-1,0);(3)![]() .
.
【解析】
(1)将一次函数变形![]() ,根据图像过定点,得到与k值无关,求出k,进而求出定点坐标;
,根据图像过定点,得到与k值无关,求出k,进而求出定点坐标;
(2)求出直线解析式,设点Q坐标为(m,m+1);分点Q在AB两侧分类讨论即可;
(3)先根据题意,求出点C坐标,点D坐标,在根据M坐标特点,得到点M所在直线解析式,求出点C对称点F,连接DF,求出DF长即可.
解:(1)一次函数![]() ,
,
∴![]() ,
,
∵不论k为何值,上式都成立,
∴![]() ,
,![]()
∴![]() ,
,![]()
∴无论 k 为何值,函数![]() 图像必过定点(
图像必过定点(![]() );
);
(2)当 k=-![]() 时,一次函数
时,一次函数![]() 为
为![]() ,
,
当x=0时,y=4;当y=0,时,-2x+4=0,x=2;
∴点A坐标为(2,0);点B坐标为(0,4);
∵点Q在在直线l2:y=x+1上,
∴设点Q坐标为(m,m+1);
①如图,当点Q位于AB右侧时,根据题意得![]()
∴![]()
解得m=3,
∴点Q坐标为(3,4);
②如图,当点Q位于AB左侧时,Q恰好位于x轴上,此时SABQ ![]() ,
,
此时Q坐标为(-1,0);
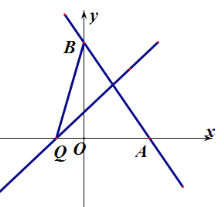
综上所述:若 /span>SABQ 6 , Q 点的坐标为(3,4)或(-1,0);
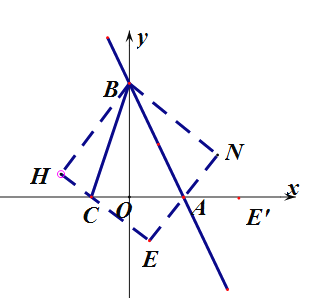
(3)如图,将△OAB沿直线AB翻折,得到△NAB,将△OCB沿直线BC翻折,得到△HCB,延长HC、NA交于点E,则四边形BHEN为正方形,且BN=BH=HE=NE=OB=4,NA=OA=2,AE=NE-AN=2,
设OC=n,则HC=n,CE=4-n,
在Rt△ACE中,![]() ,解得
,解得![]() ,
,
所以点C坐标为(![]() ) ,
) ,
如图:∵D 点在直线上![]() 上,横坐标为 1,
上,横坐标为 1,
∴y=-2×1+4=2,
所以点D坐标为(![]() );
);
∵动点 M 的坐标为(a,a),
∴点M在直线y=x上,
所以点C关于直线y=x对称的点F的坐标为(![]() ),
),
连接DF,则DF为CM+DM的最小值;
作点DG⊥y轴,垂直为G,
在Rt△DGF中,DF=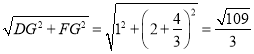 ;
;
∴CM+MD 的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠ACB=90°,BC=
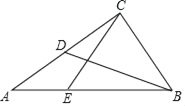
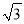 ,cot∠ABC=
,cot∠ABC=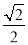 ,点D是AC的中点.
,点D是AC的中点.(1)求线段BD的长;
(2)点E在边AB上,且CE=CB,求△ACE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批甲、乙两种办公桌若干张,并且每买
 张办公桌必须买两把椅子,椅子每把
张办公桌必须买两把椅子,椅子每把 元.若学校购买
元.若学校购买 张甲种办公桌和
张甲种办公桌和 张乙种办公桌共花费
张乙种办公桌共花费 元,购买
元,购买 张甲种办公桌比购买
张甲种办公桌比购买 张乙种办公桌多花费
张乙种办公桌多花费 元。
元。(1)求甲、乙两种办公桌每张各多少元?
(2)若学校准备用不超过
 元购买甲、乙两种办公桌共
元购买甲、乙两种办公桌共 张,且甲种办公桌数量不多于乙种办公桌数量的
张,且甲种办公桌数量不多于乙种办公桌数量的 倍,请求出有哪几种购买方案?
倍,请求出有哪几种购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了将货物装入大型的集装箱卡车,需要利用传送带AB将货物从地面传送到高1.8米(即BD=1.8米)的操作平台BC上.已知传送带AB与地面所成斜坡的坡角∠BAD=37°.
(1)求传送带AB的长度;
(2)因实际需要,现在操作平台和传送带进行改造,如图中虚线所示,操作平台加高0.2米(即BF=0.2米),传送带与地面所成斜坡的坡度i=1:2.求改造后传送带EF的长度.(精确到0.1米)(参考数值:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
 ≈1.41,
≈1.41, 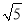 ≈2.24)
≈2.24)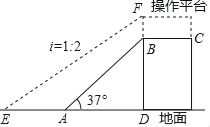
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
 ,
, 的坐标分别为
的坐标分别为 ,
, ,现同时将点
,现同时将点 ,
, 分别向上平移
分别向上平移 个单位,再向右平移
个单位,再向右平移 个单位,分别得到点
个单位,分别得到点 ,
, 的对应点
的对应点 ,
, ,连接
,连接 ,
, ,
, .(三角形可用符号
.(三角形可用符号 表示,面积用符号
表示,面积用符号 表示)
表示)
(1)直接写出点
 ,
, 的坐标.
的坐标.(2)在
 轴上是否存在点
轴上是否存在点 ,连接
,连接 ,
, ,使
,使 ,若存在,请求出点
,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(3)点
 在直线
在直线 上运动,连接
上运动,连接 ,
, .
.①若
 在线段
在线段 之间时(不与
之间时(不与 ,
, 重合),求
重合),求 的取值范围;
的取值范围;②若
 在直线
在直线 上运动,请直接写出
上运动,请直接写出 ,
, ,
, 的数量关系.
的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)求值:

(2)用消元法解方程组
 时,两位同学的解法如下:
时,两位同学的解法如下:解法一:
由①-②,得
 .
.解法二:
由②得,
 ,③
,③把①代入③,得
 .
.①反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“×”.
②请选择一种你喜欢的方法,完成解答.
(3)求不等式组
 的正整数解.
的正整数解. -
科目: 来源: 题型:
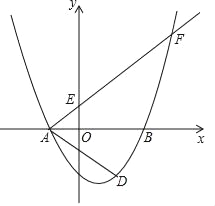
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知抛物线y=
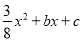 与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且
与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且 .
.(1)求这条抛物线的表达式,并写出它的对称轴;
(2)求∠FAB的余切值;
(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠AFP=∠DAB,求点P的坐标.
相关试题

