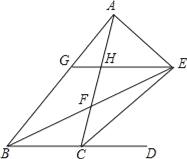
【题目】如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:
①∠BEC=![]() ∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
参考答案:
【答案】①③④.
【解析】
①根据角平分线的定义得到∠EBC=![]() ∠ABC,∠DCE=
∠ABC,∠DCE=![]() ∠ACD,根据外角的性质即可得到结论;
∠ACD,根据外角的性质即可得到结论;
②根据相似三角形的判定定理得到两个三角形相似,不能得出全等;
③由BG=GE,CH=EH,于是得到BG-CH=GE-EH=GH.即可得到结论;
④由于E是两条角平分线的交点,根据角平分线的性质可得出点E到BA、AC、BC和距离相等,从而得出AE为∠BAC外角平分线这个重要结论,再利用三角形内角和性质与外角性质进行角度的推导即可轻松得出结论.
①BE平分∠ABC,
∴∠EBC=![]() ∠ABC,
∠ABC,
∵CE平分∠ACD,
∴∠DCE=![]() ∠ACD,
∠ACD,
∵∠ACD=∠BAC+∠ABC,∠DCE=∠CBE+∠BEC,
∴∠EBC+∠BEC=![]() (∠BAC+∠ABC)=∠EBC+
(∠BAC+∠ABC)=∠EBC+![]() ∠BAC,
∠BAC,
∴∠BEC=![]() ∠BAC,故①正确;
∠BAC,故①正确;
∵②△HEF与△CBF只有两个角是相等的,能得出相似,但不含相等的边,所以不能得出全等的结论,故②错误;
③BE平分∠ABC,
∴∠ABE=∠CBE,
∵GE∥BC,
∴∠CBE=∠GEB,
∴∠ABE=∠GEB,
∴BG=GE,
同理CH=HE,
∴BGCH=GEEH=GH,
∴BG=CH+GH,
故③正确;
④过点E作EN⊥AC于N,ED⊥BC于D,EM⊥BA于M,如图,
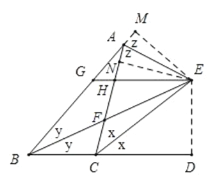
∵BE平分∠ABC,
∴EM=ED,
∵CE平分∠ACD,
∴EN=ED,
∴EN=EM,
∴AE平分∠CAM,
设∠ACE=∠DCE=x,∠ABE=∠CBE=y,∠MAE=∠CAE=z,如图,
则∠BAC=180![]() 2z,∠ACB=180
2z,∠ACB=180![]() 2x,
2x,
∵∠ABC+∠ACB+∠BAC=180![]() ,
,
∴2y+180![]() 2z+180
2z+180![]() 2x=180
2x=180![]() ,
,
∴x+z=y+90![]() ,
,
∵z=y+∠AEB,
∴x+y+∠AEB=y+90![]() ,
,
∴x+∠AEB=90![]() ,
,
即∠ACE+∠AEB=90![]() ,
,
故④正确.
故答案为:①③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图2拼成一个正方形.
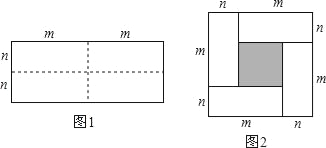
(1)直接写出图2中的阴影部分面积;
(2)观察图2,请直接写出下列三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系;
(3)根据(2)中的等量关系,解决如下问题:若p+q=9,pq=7,求(p﹣q)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元一次不等式组
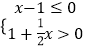 的解集在数轴上表示出来,正确的是( )
的解集在数轴上表示出来,正确的是( )
A.
B.
C.
D.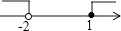
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )

A. 前2分钟,乙的平均速度比甲快
B. 5分钟时两人都跑了500米
C. 甲跑完800米的平均速度为100米/分
D. 甲乙两人8分钟各跑了800米
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x2+mx+1)(x2﹣2x+n)的展开式中不含x2和x3项.
(1)分别求m、n的值;
(2)化简求值:(m+2n+1)(m+2n﹣1)+(2m2n﹣4mn2+m3)÷(﹣m)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径CD垂直于弦AB,垂足为点E,∠ACD=22.5°,若CD=6cm,则AB的长为( )

A.4cm
B.3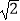 cm
cm
C.2 cm
cm
D.2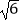 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
相关试题

