【题目】如图,△ABC内接于⊙O,BC是直径,⊙O的切线PA交CB的延长线于点P,OE∥AC交AB于点F,交PA于点E,连接BE.
(1)判断BE与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,BE=3,求AB的长.

参考答案:
【答案】(1)BE是⊙O的切线;(2)![]() .
.
【解析】试题分析:(1)结论:BE是⊙O的切线.首先证明∠OAP=90°,再证明△EOB≌△EOA,推出∠OBE=∠OAE即可解决问题.
(2)由(1)可知AB=2BF,在Rt△BEO中,∠OBE=90°,OB=4,BE=3,可得OE=![]() =5,由
=5,由![]() BEOB=
BEOB=![]() OEBF,可得BF=
OEBF,可得BF=![]() =
=![]() ,由此即可解决问题.
,由此即可解决问题.
试题解析:(1)BE是⊙O的切线.
理由:如图连接OA.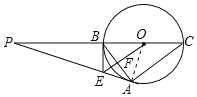
∵PA是切线,
∴PA⊥OA,
∴∠OAP=90°,
∵BC是直径,
∴∠BAC=90°,
∵OE∥AC,
∴∠OFB=∠BAC=90°,
∴OE⊥AB,
∴BF=FA,
∵OB=OA,
∴∠EOB=∠EOA,
在△EOB和△EOA中,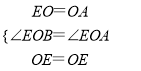 ,
,
∴△EOB≌△EOA,
∴∠OBE=∠OAE=90°,
∴OB⊥BE,
∴BE是⊙O的切线.
(2)由(1)可知AB=2BF,
在Rt△BEO中,∵∠OBE=90°,OB=8,BE=6,
∴OE=![]() =5,
=5,
∵![]() BEOB=
BEOB=![]() OEBF,
OEBF,
∴BF=![]() =
=![]() ,
,
∴AB=2BF=![]()
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为12cm,弦AB=12
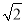 cm.
cm.(1)求圆心O到弦AB的距离.
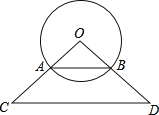
(2)若弦AB恰好是△OCD的中位线,以CD中点E为圆点,R为半径作⊙E,当⊙O和⊙E相切时,求R的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图中的折线ABC表示某汽车的耗油量y(L/km)与速度x(km/h)之间的函数关系(30≤x≤120).已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
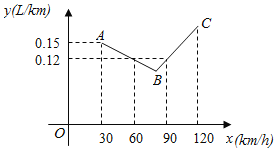
(1)当30≤x≤120时,求y与x之间的函数表达式;
(2)该汽车的速度是多少时,耗油量最低?最低是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
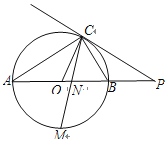
(1)求证:PC是⊙O的切线;
(2)求证:BC=
 AB;
AB;(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN
 MC的值.
MC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形ABC中,AB⊥AC,AD⊥BC,EF⊥BC,∠1=∠2.
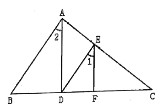
(1)求证:DE⊥AC
(2)请直接写出图中所有与∠1的和为90°的角
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠MAN=30°,点B在射线AM上,且 AB=6,点C在射线AN上.

(1)若△ABC是直角三角形,求AC的长;
(2)若△ABC是等腰三角形,则满足条件的C点有 个;
(3)设BC=x,当△ABC唯一确定时, 直接写出
 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.
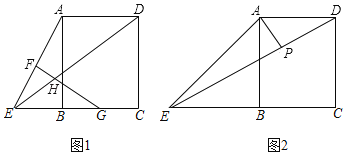
(1)求证:HE=HG;
(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求PQ与PB的数量关系,并说明理由.
相关试题

